
已知椭圆的两个焦点坐标分别是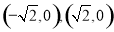 ,并且经过点
,并且经过点 .
.
(1)求椭圆的标准方程;
(2)若斜率为 的直线
的直线 经过点
经过点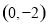 ,且与椭圆交于不同的两点
,且与椭圆交于不同的两点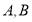 ,求
,求  面积的最大值.
面积的最大值.
(1)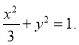 (2)
(2)
【解析】
试题分析:(1)由椭圆的两个焦点坐标分别是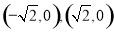 ,即椭圆的焦半径
,即椭圆的焦半径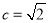 ,并且经过点
,并且经过点 ,所以根据椭圆的定义求得椭圆的长半轴
,所以根据椭圆的定义求得椭圆的长半轴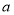 ,再根据
,再根据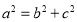 即可求出椭圆的短半轴
即可求出椭圆的短半轴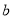 的值.从而得到椭圆的标准方程.
的值.从而得到椭圆的标准方程.
(2)假设过点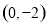 的直线,联立方程,韦达定理以及弦长公式表示出弦长.再用点到直线的距离,即可得到高.再通过换元求得最值.
的直线,联立方程,韦达定理以及弦长公式表示出弦长.再用点到直线的距离,即可得到高.再通过换元求得最值.
试题解析:(1)设椭圆的标准方程为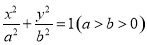 ,有椭圆的定义可得
,有椭圆的定义可得
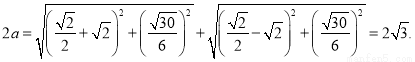
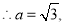 又
又
故椭圆的标准方程为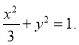 4分.
4分.
(2)设直线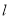 的方程为
的方程为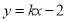 ,
,
由 得
得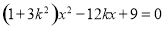 ,依题意
,依题意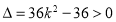 ,
,
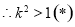 6分
6分
设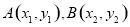 ,
,
则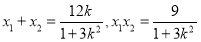 , 7分
, 7分
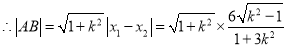 , 8分
, 8分
由点到直线的距离公式得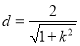 , 9分
, 9分
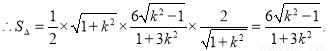 10分
10分
设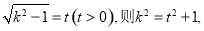
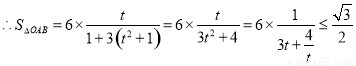 ,
,
当且仅当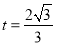 时,上式取等号,
时,上式取等号,
所以,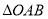 面积的最大值为
面积的最大值为 12分
12分
考点:1.椭圆的标准方程.2.直线与椭圆的位置关系.3.点到直线的距离.4.最值的求法.


科目:高中数学 来源:2015届河北省石家庄市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
某人上班途中要经过三个有红绿灯的路口,设遇到红灯的事件相互独立,且概率都是0.3,则此人上班途中遇到红灯的次数的期望为( ).
A.0.3 B.0.33 C.0.9 D.0.7
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市五校联合体高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
已知不等式组 表示的平面区域恰好被圆C:
表示的平面区域恰好被圆C: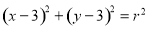 所覆盖,则实数k的值是( )
所覆盖,则实数k的值是( )
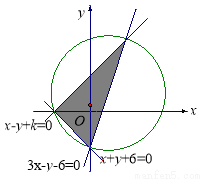
A.3 B.4 C.5 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com