
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率;
(2)求ξ的分布列.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-1函数的概念、定义域和值域(解析版) 题型:选择题
如图,是张大爷晨练时所走的离家距离(y)与行走时间(x)之间的函数关系的图象.若用黑点表示张大爷家的位置,则张大爷散步行走的路线可能是( )


查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:填空题
已知函数f(x)=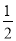 x-
x-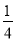 sinx-
sinx-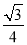 cosx的图象在点A(x0,y0)处的切线斜率为1,则tanx0=________.
cosx的图象在点A(x0,y0)处的切线斜率为1,则tanx0=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-8n次独立重复实验与二项分布(解析版) 题型:选择题
在高三的一个班中,有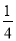 的学生数学成绩优秀,若从班中随机找出5名学生,那么数学成绩优秀的学生数ξ~B(5,
的学生数学成绩优秀,若从班中随机找出5名学生,那么数学成绩优秀的学生数ξ~B(5,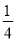 ),则P(ξ=k)取最大值的k值为( )
),则P(ξ=k)取最大值的k值为( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:填空题
某毕业生参加人才招聘会,分别向甲、乙、丙三个公司投递了个人简历.假定该毕业生得到甲公司面试的概率为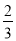 ,得到乙、丙两公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记X为该毕业生得到面试的公司个数.若P(X=0)=
,得到乙、丙两公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记X为该毕业生得到面试的公司个数.若P(X=0)=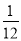 ,则随机变量X的数学期望E(X)=________.
,则随机变量X的数学期望E(X)=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:选择题
甲乙两人分别独立参加某高校自主招生面试,若甲、乙能通过面试的概率都是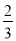 ,则面试结束后通过的人数X的数学期望是( )
,则面试结束后通过的人数X的数学期望是( )
A. B.
B. C.1 D.
C.1 D.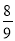
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-6几何概型(解析版) 题型:解答题
已知复数z=x+yi(x,y∈R)在复平面上对应的点为M.
(1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中随机取一个数作为y,求复数z为纯虚数的概率;
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组: 所表示的平面区域内的概率.
所表示的平面区域内的概率.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-3二项式定理(解析版) 题型:选择题
(2-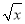 )8展开式中不含x4项的系数的和为( )
)8展开式中不含x4项的系数的和为( )
A.-1 B.0 C.1 D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com