练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】预计某地区明年从年初开始的前 个月内，对某种商品的需求总量 （万件）近似满足： ，且 ）
    （1）写出明年第 个月的需求量 （万件）与月份 的函数关系式，并求出哪个月份的需求量超过 万件；
    （2）如果将该商品每月都投放到该地区 万件（不包含积压商品），要保证每月都满足供应， 应至少为多少万件？（积压商品转入下月继续销售）

    【答案】
    （1） 时， （万件）

    当 时，

    且 ．

    由 即

    化简得 ，解得 .

    又 ， ．

    答：第 月份的需求量超过 万件．


    （2）保证每月都满足供应，则 对于 ， 恒成立

    时 取最大值

    答：每月至少应投放 万件．


    【解析】分析：（1）利用 导出 的解析式,再解不等式 . （2）关键列出关系式 对于 ， 恒成立,即 , , ,都成立.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，网格纸上小正方形的边长为1，粗线画出的是某个四面体的三视图，则该四面体的表面积为（ ）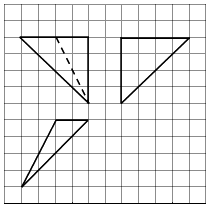

    A.8+8 +4
    B.8+8 +2
    C.2+2 +
    D. + +

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， （其中， ），且函数的图象在点处的切线与函数的图象在点处的切线重合．

    （1）求实数， 的值；

    （2）记函数，是否存在最小的正常数，使得当时，对于任意正实数，不等式恒成立？给出你的结论，并说明结论的合理性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和Sn=n2﹣n，数列{bn}的前n项和Tn=4﹣bn ．
    （1）求数列{an}和{bn}的通项公式；
    （2）设cn= anbn ， 求数列{cn}的前n项和Rn的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设△ABC的内角A、B、C所对的边分别为a、b、c，已知a=1，b=2，cosC=
    （1）求△ABC的周长；
    （2）求cos（A﹣C）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面是正方形，每条侧棱的长都是底面边长的倍，为侧棱上的点．

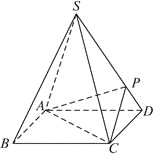
    （1）求证：．

    （2）若⊥平面，求二面角的大小．

    （3）在（2）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC?若存在，求SE∶EC的值；若不存在，试说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】当 时，不等式 恒成立，则实数a的取值范围是（ ）
    A.[-5,-3]
    B.[-6,1]
    C.[-6,-2]
    D.[-4,-3]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，直三棱柱中， ， 为的中点， 为的中点.

    （1）求证： 面；

    （2）若面，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知曲线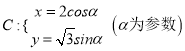和定点， 是此曲线的左、右焦点，以原点为极点，以轴正半轴为极轴，建立极坐标系.

    (1)求直线的极坐标方程；

    (2)经过点且与直线垂直的直线交此圆锥曲线于两点，求的值.

    查看答案和解析>>

    同步练习册答案