
分析 (1)直接利用直线的一般式方程转化为求截距式方程,然后求解在x轴、y轴上的截距;
(2)设出平行于直线x-y+2=0的直线方程,利用与它的距离为$\sqrt{2}$,求解直线的方程;
(3)求出直线的斜率,中点坐标,利用点斜式求解即可.
解答 (本小题满分12分)
解:(1)将2x+5y-20=0化为截距式$\frac{x}{10}$+$\frac{y}{4}$=1
由此可知此直线在x轴、y轴上的截距分别为10与4
(或直接令x=0,y=0得截距)-------------------------------------(4分)
(2)因为所求直线平行于直线x-y+2=0
所以可设所求直线方程为x-y+c=0
这两条直线间的距离
d=$\frac{|c-2|}{\sqrt{12+(-1)2}}$=$\sqrt{2}$
解c=0或c=4
直线方程为x-y=0或x-y+4=0-----------------------(8分)
(3)直线MN的斜率kMN=$\frac{4-(-1)}{-5-7}$=-$\frac{5}{12}$
MN的垂直平分线的斜率k=-$\frac{1}{kMN}$=$\frac{12}{5}$
MN的中点坐标(1,$\frac{3}{2}$)
所以线段MN的垂直平分线的方程为y-$\frac{3}{2}$=$\frac{12}{5}$(x-1)
整理得24x-10y-9=0------------------------------------------------(12分)
点评 本题考查直线方程的求法与应用,是基本知识的考查.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,0),(1,0) | B. | (-6,0),(6,0) | C. | $(-\sqrt{6},0),(\sqrt{6},0)$ | D. | $(0,-\sqrt{6}),(0,\sqrt{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
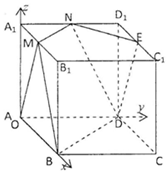 如图,棱长为a的正方体ABCD-A1B1C1D1中,点M,N,E分别是棱A1B1,A1D1,C1D1的中点.
如图,棱长为a的正方体ABCD-A1B1C1D1中,点M,N,E分别是棱A1B1,A1D1,C1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
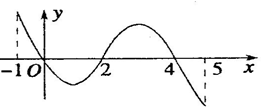 已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -4 | C. | 0 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com