
【题目】已知![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() 时,不等式
时,不等式![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】
(1)将a=1代入f(x)中,去绝对值后分别解不等式即可;
(2)x∈(0,1)时,不等式f(x)<x+2恒成立等价于当x∈(0,1)时,|ax-1|<1恒成立,然后分a≤0和a>0讨论即可.
解:(1)解法1:当![]() 时,不等式
时,不等式![]() 可化简为
可化简为![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,无解;
,无解;
当![]() 时,
时,![]() ,解得
,解得![]() ,所以
,所以![]() ﹒
﹒
综上,不等式![]() 的解集为
的解集为![]() .
.
解法2:当![]() 时,
时,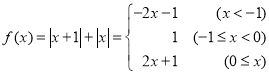
当![]() 时,
时,![]() ,解得
,解得![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,无解;
,无解;
当![]() 时,
时,![]() ,解得
,解得![]() ,所以
,所以![]() .
.
综上,不等式![]() 的解集为
的解集为![]() .
.
(2)解法1:当![]() 时,不等式
时,不等式![]() 可化简为
可化简为![]() .
.
令![]() ,则
,则![]() 的图像为过定点
的图像为过定点![]() 斜率为a的一条直线,
斜率为a的一条直线,
数形结合可知,当![]() 时,
时,![]() 在
在![]() 上恒成立.
上恒成立.
所以,所求a的取值范围为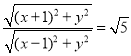
解法2:当![]() 时,不等式
时,不等式![]() 可化简为
可化简为![]() .
.
由不等式的性质得![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
当![]() 时,
时,![]() ,不等式
,不等式![]() 不恒成立;
不恒成立;
为使不等式![]() 恒成立,则
恒成立,则![]() .
.
综上,所求a的取值范围为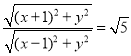 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,F为椭圆C的右焦点,A是右准线与x轴的交点,且AF=1.
,F为椭圆C的右焦点,A是右准线与x轴的交点,且AF=1.

(1)求椭圆C的方程;
(2)过椭圆C上顶点B的直线l交椭圆另一点D,交x轴于点M,若![]() ,求直线l的方程;
,求直线l的方程;
(3)设点![]() ,过点F且斜率不为零的直线m与椭圆C交于S,T两点,直线TQ与直线x=2交于点S1,试问
,过点F且斜率不为零的直线m与椭圆C交于S,T两点,直线TQ与直线x=2交于点S1,试问![]() 是否为定值?若是,求出这个定值,若不是,请说明理由.
是否为定值?若是,求出这个定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合![]() ,
,![]() ,
,![]() ,
,![]() .集合
.集合![]() 中的元素个数记为
中的元素个数记为![]() .规定:若集合
.规定:若集合![]() 满足
满足![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(I)已知集合![]() ,
,![]() ,写出
,写出![]() ,
,![]() 的值;
的值;
(II)已知集合![]() ,
,![]() 为等比数列,
为等比数列,![]() ,且公比为
,且公比为![]() ,证明:
,证明:![]() 具有性质
具有性质![]() ;
;
(III)已知![]() 均有性质
均有性质![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由
年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由![]() 年底的
年底的![]() 下降到
下降到![]() 年底的
年底的![]() ,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,
,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,![]() 年至
年至![]() 年我国贫困发生率的数据如下表:
年我国贫困发生率的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的![]() 个贫困发生率数据中任选两个,求两个都低于
个贫困发生率数据中任选两个,求两个都低于![]() 的概率;
的概率;
(2)设年份代码![]() ,利用线性回归方程,分析
,利用线性回归方程,分析![]() 年至
年至![]() 年贫困发生率
年贫困发生率![]() 与年份代码
与年份代码![]() 的相关情况,并预测
的相关情况,并预测![]() 年贫困发生率.
年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
 (
(![]() 的值保留到小数点后三位)
的值保留到小数点后三位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠DAB=60°.
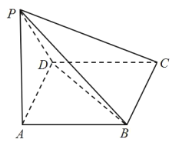
(1)证明:AD⊥PB.
(2)若PB=![]() ,AB=PA=2,求三棱锥P-BCD的体积。
,AB=PA=2,求三棱锥P-BCD的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人承揽一项业务,需做文字标牌4个,绘画标牌5个,现有两种规格的原料,甲种规格每张3m2,可做文字标牌1个,绘画标牌2个,乙种规格每张2m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,己知圆
中,己知圆![]() ,且圆
,且圆![]() 被直线
被直线![]() 截得的弦长为2.
截得的弦长为2.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 的切线
的切线![]() 在
在![]() 轴和
轴和![]() 轴上的截距相等,求切线
轴上的截距相等,求切线![]() 的方程;
的方程;
(3)若圆![]() 上存在点
上存在点![]() ,由点
,由点![]() 向圆
向圆![]() 引一条切线,切点为
引一条切线,切点为![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com