
| 5 |
| 2 |
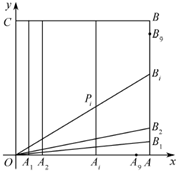 ��1��֤���������⣬��Ai(i��N*��1��i��9)����x�ᴹֱ��ֱ�߷���Ϊ
��1��֤���������⣬��Ai(i��N*��1��i��9)����x�ᴹֱ��ֱ�߷���Ϊ| i |
| 10 |
|
| 1 |
| 10 |
|
|
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| tan�� |
| 5 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
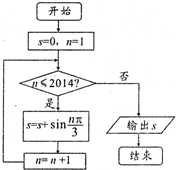
A��-
| ||||
B��-
| ||||
C��
| ||||
D��
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1+a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| y2 |
| a2 |
| x2 |
| b2 |
| NA |
| AF |
| NB |
| BF |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a+c |
| b |
| sinA-sinB |
| sinA-sinC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| QR |
| RS |
| QS |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
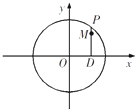 ��ͼ����P��Բx2+y2=25�ϵĶ��㣬��D��P��x���ϵ�ͶӰ��MΪPD��һ�㣬��|MD|=
��ͼ����P��Բx2+y2=25�ϵĶ��㣬��D��P��x���ϵ�ͶӰ��MΪPD��һ�㣬��|MD|=| 4 |
| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
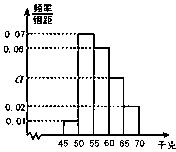 Ϊ�˽�ѧ��������״����ijУ�����ȡ��һ��ѧ���������أ���ͳ�ƣ�����ѧ�����������ݣ���λ��ǧ�ˣ�ȫ������45��70֮�䣮�����ݷֳ�����5�飺��1��[45��50������2��[50��55������3��[55��60������4��[60��65������5��[65��70]���õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ����a=
Ϊ�˽�ѧ��������״����ijУ�����ȡ��һ��ѧ���������أ���ͳ�ƣ�����ѧ�����������ݣ���λ��ǧ�ˣ�ȫ������45��70֮�䣮�����ݷֳ�����5�飺��1��[45��50������2��[50��55������3��[55��60������4��[60��65������5��[65��70]���õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ����a=�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com