
| a+c |
| b |
| sinA-sinB |
| sinA-sinC |
| a+c |
| b |
| sinA-sinB |
| sinA-sinC |
| a-b |
| a-c |
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
| A、y=3(x-1)2-2 |
| B、y=3(x+1)2+2 |
| C、y=3(x+1)2-2 |
| D、y=-3(x+1)2-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
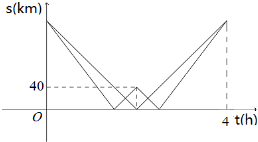 A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行
A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com