
分析 (1)利用极坐标方程、直角坐标方程间的互化公式,把曲线C的极坐标方程化为直角坐标方程;利用参数方程、直角坐标方程间的互化公式,把直线l的参数方程化为直角坐标方程,再化为极坐标方程.
(2)把直线l的标准的参数方程代入曲线返程,利用韦达定理以及参数的几何意义,求得|PA|•|PB|的值.
解答 解:(1)由$ρ=4cos(θ-\frac{π}{3})$得,$ρ=4cosθcos\frac{π}{3}+4sinθsin\frac{π}{3}=2cosθ+2\sqrt{3}sinθ$,即 ρ2=2ρcosθ+2$\sqrt{3}$ρsinθ,
所以曲线C的直角坐标方程为${x^2}+{y^2}-2x-2\sqrt{3}y=0$,即${(x-1)^2}+{(y-\sqrt{3})^2}=4$.
∵直线l的参数方程为$\left\{\begin{array}{l}x=2+\sqrt{3}t\\ y=\sqrt{3}+t\end{array}\right.$∴直线l的普通方程为$x-\sqrt{3}y+1=0$,
∴直线l的极坐标方程为$ρcosθ-\sqrt{3}ρsinθ+1=0$.
(2)$\left\{\begin{array}{l}x=2+\sqrt{3}t\\ y=\sqrt{3}+t\end{array}\right.$化为标准参数方程$\left\{\begin{array}{l}{x=2+\frac{\sqrt{3}}{2}t}\\{y=\sqrt{3}+\frac{1}{2}t}\end{array}\right.$,代入曲线C:${x^2}+{y^2}-2x-2\sqrt{3}y=0$得,t2+$\sqrt{3}$t-3=0,
设A、B两点对应的参数分别为t1、t2,则t1•t2=-3,∴|PA|•|PB|=|t1•t2|=3.
点评 本题主要考查参数方程、极坐标方程、直角坐标方程间的互化,参数的几何意义,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | p假q假 | B. | p真q假 | C. | p假q真 | D. | p真q真 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
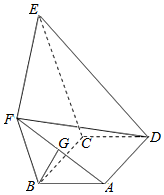 如图,四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BF⊥BC,CE=2BF=2AB=4,∠ABF=DCE=120°,G是AF中点.
如图,四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BF⊥BC,CE=2BF=2AB=4,∠ABF=DCE=120°,G是AF中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y与x具有正线性相关关系 | |
| B. | 回归直线必过点($\overline{x}$,$\overline{y}$) | |
| C. | 该女士月收入增加1000元,则其发红包的数量约增加9个 | |
| D. | 该女士月收入为3000元,则可断定其发红包的数量为27个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | -2 | -1 | 0 | 1 | 2 |
| y | 5 | 4 | 2 | 2 | 1 |
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| y | k | 3.35 | 5.65 | 8.2 |
| A. | 1 | B. | 0.95 | C. | 0.9 | D. | 0.85 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com