练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知f（x）=ax2+bx+c（a≠0）经过点（﹣1，0），（0，0），（1，2）．
    （1）求f（x）的解析式；
    （2）若数列{an}的前n项和Sn满足Sn=f（n），求{an}的通项公式．

    【答案】
    （1）解：将（﹣1，0），（0，0），（1，2）代入f（x）=ax2+bx+c得：

    ，解得 ，

    ∴f（x）=x2+x；


    （2）解：由（1）得：Sn=n2+n，

    ∴an=Sn﹣Sn﹣1=n2﹣n﹣[（n﹣1）2+（n﹣1）]=2n，

    即{an}的通项公式是：an=2n


    【解析】（1）根据待定系数法求出a，b，c的值，从而求出函数的解析式即可；（2）求出Sn ， 从而求出an即可．
    【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】【2018河北保定市上学期期末调研】已知点到点的距离比到轴的距离大1．

    （I）求点的轨迹的方程；

    （II）设直线： ，交轨迹于、两点， 为坐标原点，试在轨迹的部分上求一点，使得的面积最大，并求其最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法：

    ①函数的单调增区间是；

    ②若函数定义域为且满足，则它的图象关于轴对称；

    ③函数的值域为；

    ④函数的图象和直线的公共点个数是，则的值可能是；

    ⑤若函数在上有零点，则实数的取值范围是.

    其中正确的序号是_________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，，．

    （1）求证：；

    （2）试在线段上找一点，使平面，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某医药研究所开发一种新药, 成年人按规定的剂量服用后, 每毫升血液中的含药量(微克)与时间(小时)之间关系满足如图所示的曲线.

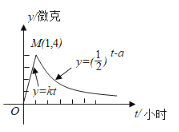
    (1)写出关于的函数关系式:；

    (2)据进一步测定: 每毫升血液中的含药量不少于微克时, 治疗疾病有效. 求服药一次后治疗疾病有效的时间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设有关于x的一元二次方程x2+2ax+b2=0.

    (1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.

    (2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=
    （1）求函数f（x）的定义域A；
    （2）设B={x|﹣1＜x＜2}，当实数a、b∈（B∩RA）时，证明： |．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=2x，g（x）是一次函数，并且点（2，2）在函数f[（g（x）]的图象上，点（2，5）在函数g[f（x）]的图象上，则g（x）的解析式为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xoy中，曲线C1： （t为参数，t≠0），其中0≤α＜π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，曲线C3：ρ=2 cosθ．
    （1）求C2与C3交点的直角坐标；
    （2）若C2与C1相交于点A，C3与C1相交于点B，求|AB|的最大值．

    查看答案和解析>>

    同步练习册答案