
【题目】某校从参加高一年级期中考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…,[80,90),[90,100],然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题: 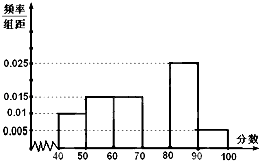
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及60分以上为及格)和平均分;
(3)把从[80,90)分数段选取的最高分的两人组成B组,[90,100]分数段的学生组成C组,现从B,C两组中选两人参加科普知识竞赛,求这两个学生都来自C组的概率.
【答案】
(1)解:分数在[70,80)内的频率为:
1﹣(0.05+0.1+0.15+0.15+0.25)=0.30
![]() =
= ![]() =0.03,
=0.03,
补全后的直方图如下:
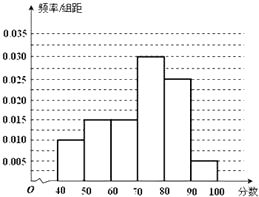
(2)解:由题意60分以上的各组频率和为:
(0.015+0.03+0.025+0.005)×10=0.75,
故这次考试的及格率约为75%,
由45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71,
得本次考试中的平均分约为71:
(3)解:由已知可得C组共有学生60×10×0.005=3人,
则从B,C两组中选两人参加科普知识竞赛共有 ![]() =10种不同情况,
=10种不同情况,
其中这两个学生都来自C组有 ![]() =3种不同情况,
=3种不同情况,
∴这两个学生都来自C组的概率P= ![]() .
.
【解析】(1)频率分布直方图中,小矩形的面积等于这一组的频率,而频率的和等于1,可求出分数在[70,80)内的频率,即可求出矩形的高,补全这个频率分布直方图.(2)累加60分及60分以上的各组频率可得到这次考试的及格率,再在同一组数据用该组区间的中点值作为代表,将中点值与每一组的频率相差再求出它们的和即可求出本次考试的平均分.(3)分别求出从B,C两组中选两人的基本事件总数和这两个学生都来自C组的基本事件个数,代入古典概型概率公式,可得答案.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
, ![]() ,
, ![]() ,
, ![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下:
甲说:“![]() 或
或![]() 作品获得一等奖”
作品获得一等奖”
乙说:“![]() 作品获得一等奖”
作品获得一等奖”
丙说:“![]() ,
, ![]() 两项作品未获得一等奖”
两项作品未获得一等奖”
丁说:“![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
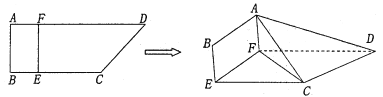
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在
分别在![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使
折起,使![]() .
.
(1)若![]() ,在折叠后的线段
,在折叠后的线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(2)求三棱锥![]() 的体积的最大值,并求出此时点
的体积的最大值,并求出此时点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(x、y)满足
(1)若x∈{0,1,2,3,4,5},y∈{0,1,2,3,4},则求y≥x的概率.
(2)若x∈[0,5],y∈[0,4],则求x>y的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
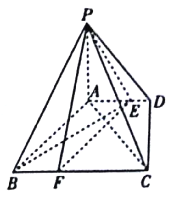
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知E、F分别在正方体ABCD﹣A1B1C1D1的棱BB1、CC1上,且B1E=2EB,CF=2FC1 , 则面AEF与面ABC所成的二面角的正切值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与圆
与圆![]() 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线![]() 对称.
对称.
(1)求m,k的值;
(2)若直线![]() 与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com