练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．如图，AT切⊙O于T，若AT=6，AE=3，AD=4，DE=2，则BC等于（　　）
    A．3B．4C．6D．8

    分析 利用AT为⊙O的切线，求出AT，证明△EAD∽△CAB，可得$\frac{DE}{BC}=\frac{AE}{AC}$，即可求出BC．

    解答 解：∵AT为⊙O的切线，∴AT2=AD•AC．
    ∵AT=6，AD=4，∴AC=9．
    ∵∠ADE=∠B，∠EAD=∠CAB，
    ∴△EAD∽△CAB，即$\frac{DE}{BC}=\frac{AE}{AC}$，
    ∴BC=$\frac{DE•AC}{AE}$=$\frac{2×9}{3}$=6．
    故选：C．

    点评 本题考查切割线定理，考查三角形相似的判断与性质，考查学生的计算能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．如图1，在平行四边形ABCD中，AB=2AD，E，F分别为AB，CD的中点，沿EF将四边形AEFD折起到新位置变为四边形A′EFD′，使A′B=A′F（如图2所示）．
    （1）证明：A′E⊥BF；
    （2）若∠BAD=60°，A′E=$\sqrt{2}$A'B=2，求二面角A′-EF-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

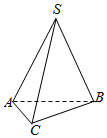    14．如图，在三棱锥S-ABC中，底面ABC为等边三角形，SA=SB=$\sqrt{10}$，AB=2，平面SAB⊥平面ABC，则SC与平面ABC所成角的大小是60°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．在空间直角坐标系中，$\overrightarrow{i}$=（1，0，0），$\overrightarrow{j}$=（0，1，0），$\overrightarrow{k}$=（0，0，1），则与$\overrightarrow{i}$，$\overrightarrow{j}$，$\overrightarrow{k}$所成角都相等的单位向量为（　　）
    A．（1，1，1）B．（$\frac{1}{3}$，$\frac{1}{3}$，$\frac{1}{3}$）
    C．（$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$）D．（$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$）或（-$\frac{\sqrt{3}}{3}$，-$\frac{\sqrt{3}}{3}$，-$\frac{\sqrt{3}}{3}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．不等式组$\left\{\begin{array}{l}-2{x^2}+x+1＜0\\（x-1）（x-2）（x-3）＞0\end{array}\right.$的解集是（　　）
    A．（-∞，$\frac{1}{2}$）∪（1，2）B．（1，2）∪（3，+∞）C．（-∞，$\frac{1}{2}$）∪（1，+∞）D．（2，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

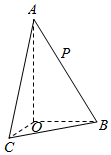    8．如图所示，AO⊥平面BOC，∠OAB=30°，△AOC与△AOB全等，且二面角B-AO-C是直二面角，动点P在线段AB上，则CP与平面AOB所成角的正切的最大值为（　　）
    A．1B．$\sqrt{3}$C．$\frac{\sqrt{3}}{3}$D．$\frac{2\sqrt{3}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．非零向量$\overrightarrow{m}$，$\overrightarrow{n}$的夹角的余弦值为$\frac{1}{3}$，且4|$\overrightarrow{m}$|=3|$\overrightarrow{n}$|，若$\overrightarrow{n}$⊥（t$\overrightarrow{m}$+$\overrightarrow{n}$），则实数t为（　　）
    A．4B．-4C．$\frac{4}{9}$D．-$\frac{4}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．经调查统计，在某十字路中红亮起时排队等候的车辆数及相应概率如下：
    排队车辆数0123≥4
    概率x0.30.30.20.1
    则该十字路口红灯亮起时至多有2辆车排队等候的概率是（　　）
    A．0.7B．0.6C．0.4D．0.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．设a，b，c是正整数，且a∈[70，80），b∈[80，90），c∈[90，100]，当数据a，b，c的方差最小时，a+b+c的值为（　　）
    A．252或253B．253或254C．254或255D．267或268

    查看答案和解析>>

    同步练习册答案