
在平面直角坐标系xOy中,已知圆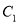 :
: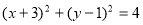 和圆
和圆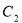 :
: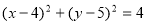

(1)若直线l过点A(4,0),且被圆C1截得的弦长为2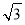 ,求直线l的方程;
,求直线l的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线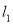 和
和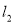 ,它们分别与圆
,它们分别与圆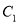 和圆
和圆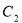 相交,且直线
相交,且直线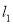 被圆
被圆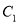 截得的弦长与直线
截得的弦长与直线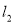 被圆
被圆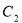 截得的弦长相等,试求所有满足条件的点P的坐标.
截得的弦长相等,试求所有满足条件的点P的坐标.
(1) 直线 的方程为
的方程为 或
或 ;(2) 点
;(2) 点 或点
或点 .
.
【解析】
试题分析:在解决与圆相关的弦长问题时,一般有三种方法:一是直接求出直线与圆的交点坐标,再利用两点间的距离公式得出;二是不求交点坐标,用一元二次方程根与系数的关系得出,即设直线的斜率为k,直线与圆联立消去y后得到一个关于x的一元二次方程再利用弦长公式求解,三是利用圆中半弦长、弦心距及半径构成的直角三角形来求.对于圆中的弦长问题,一般利用第三种方法比较简捷.本题所用方法就是第三种方法.
(1)直线 过点
过点 ,故可以设出直线
,故可以设出直线 的点斜式方程,又由直线被圆
的点斜式方程,又由直线被圆 截得的弦长为
截得的弦长为 ,根据半弦长、半径、弦心距满足勾股定理,求出弦心距,即圆心到直线的距离,得到一个关于直线斜率
,根据半弦长、半径、弦心距满足勾股定理,求出弦心距,即圆心到直线的距离,得到一个关于直线斜率 的方程,解方程求出
的方程,解方程求出 值,可求直线
值,可求直线 的方程.
的方程.
(2)与(1)相同,设出过 点的直线
点的直线 与
与 的点斜式方程,由于两直线斜率为1,且直线
的点斜式方程,由于两直线斜率为1,且直线 被圆
被圆 截得的弦长与直线
截得的弦长与直线 被圆
被圆 截得的弦长相等,得到一个关于直线斜率
截得的弦长相等,得到一个关于直线斜率 的方程,解方程求出
的方程,解方程求出 值,代入即得直线
值,代入即得直线 与
与 的方程.
的方程.
试题解析:(1)由于直线 与圆
与圆 不相交,所以直线
不相交,所以直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为 ,圆
,圆 的圆心
的圆心 到直线
到直线 的距离为
的距离为 ,
,
因为直线 被圆
被圆 截得的弦长为
截得的弦长为 ,
,
 ,
,
即 或
或 ,
,
所以直线 的方程为
的方程为 或
或 (5分)
(5分)
(2)设点 满足条件,不妨设直线
满足条件,不妨设直线 的方程为
的方程为 ,
,
则直线 的方程为
的方程为 ,因为
,因为 和
和 的半径相等,及直线
的半径相等,及直线 被圆
被圆 截得的弦长与直线
截得的弦长与直线 被圆
被圆 截得的弦长相等,所以圆
截得的弦长相等,所以圆 的圆心到直线
的圆心到直线 的距离和圆
的距离和圆 的圆心到直线
的圆心到直线 的距离相等,
的距离相等,
即 (8分)
(8分)
整理得: 即
即 ,因为
,因为 的取值有无穷多个,
的取值有无穷多个,
所以 (12分)
(12分)
解得
这样点 只可能是点
只可能是点 或点
或点 .
.
经检验点 和
和 满足题目条件. (14分)
满足题目条件. (14分)
考点:本题考查直线与圆的位置关系.


科目:高中数学 来源:2016届贵州遵义湄潭中学高一上学期期末考试数学试卷(解析版) 题型:选择题
函数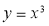 ( )
( )
A.是偶函数,且在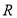 上是单调减函数
上是单调减函数
B.是奇函数,且在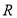 上是单调减函数
上是单调减函数
C.是偶函数,且在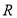 上是单调增函数
上是单调增函数
D.是奇函数,且在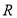 上是单调增函数
上是单调增函数
查看答案和解析>>
科目:高中数学 来源:2016届福建省高一上学期期中考试数学试卷(解析版) 题型:选择题
若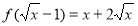 ,则f(x)=
,则f(x)=
A.x2+4x+3(x∈R) B.x2+4x(x∈R)
C.x2+4x(x≥-1) D.x2+4x+3(x≥-1)
查看答案和解析>>
科目:高中数学 来源:2016届福建省宁德市高一上学期期末考试数学试卷(解析版) 题型:选择题
某学校有教师160人,其中高级、中级和初级职称的教师分别有32人、64人和64人.为了了解教师的身体状况,用分层抽样方法抽取了一个容量为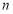 的样本.若所抽取的样本中中级职称教师有16人,则
的样本.若所抽取的样本中中级职称教师有16人,则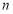 的值为
的值为
A.32 B.36 C.38 D.40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com