
【题目】矩形ABCD中,AB<BC,将△ABC沿着对角线AC所在的直线进行翻折,记BD中点为M,则在翻折过程中,下列说法错误的是( ) 
A.存在使得AB⊥DC的位置
B.存在使得AB⊥BD的位置
C.存在使得AM⊥DC的位置
D.存在使得AM⊥AC的位置
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
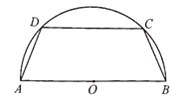
【题目】如图,有一块半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是![]() 的直径,上底CD的端点在圆周上,为研究这个梯形周长的变化情况,有以下两种方案:方案一:设腰长
的直径,上底CD的端点在圆周上,为研究这个梯形周长的变化情况,有以下两种方案:方案一:设腰长![]() ,周长为
,周长为![]() ;方案二:设
;方案二:设![]() ,周长为
,周长为![]() ,当x,
,当x,![]() 在定义域内增大时
在定义域内增大时![]()
![]()
A. ![]() 先增大后减小,
先增大后减小,![]() 先减小后增大
先减小后增大
B. ![]() 先增大后减小,
先增大后减小,![]() 先增大后减小
先增大后减小
C. ![]() 先减小后增大,
先减小后增大,![]() 先增大后减小
先增大后减小
D. ![]() 先减小后增大,
先减小后增大,![]() 先减小后增大
先减小后增大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 在曲线
在曲线![]() 上,从原点向
上,从原点向![]() 移动,如果直线
移动,如果直线![]() ,曲线
,曲线![]() 及直线
及直线![]() 所围成的两个阴影部分的面积分别记为
所围成的两个阴影部分的面积分别记为![]() ,
,![]() ,如图所示.
,如图所示.
(1)当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)当![]() 有最小值时,求点
有最小值时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①残差可用来判断模型拟合的效果;
②设有一个回归方程:![]() ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;
③线性回归直线:![]() 必过点
必过点![]() ;
;
④在一个![]() 列联表中,由计算得
列联表中,由计算得![]() ,则有
,则有![]() 的把握确认这两个变量间有关系(其中
的把握确认这两个变量间有关系(其中![]() );
);
其中错误的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张同学计划在期末考试结束后,和其他小伙伴一块儿外出旅游,增长见识.旅行社为他们提供了省内的都江堰、峨眉山、九寨沟和省外的丽江古城,黄果树瀑布和凤凰古城这六个景点,由于时间和距离等原因,只能从中任取4个景点进行参观,其中黄果树瀑布不能第一个参观,且最后参观的是省内景点,则不同的旅游顺序有( )
A. 54种 B. 72种 C. 120种 D. 144种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对该班22名学生进行了作业量的调查,在喜欢玩电脑游戏的12人中,有10人认为作业多,2人认为作业不多;在不喜欢玩电脑游戏的10人中,有3人认为作业多,7人认为作业不多.
(1)根据以上数据建立一个![]() 列联表.
列联表.
(2)对于该班学生,能否在犯错误概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关系?
下面临界值表仅供参考:
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表提供了工厂技术改造后某种型号设备的使用年限![]() 和所支出的维修费
和所支出的维修费![]() (万元)的几组对照数据:
(万元)的几组对照数据:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式: ,
,![]() .
.
(1)若知道![]() 对
对![]() 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com