
分析 (Ⅰ)由抛物线的性质,求得x=-1是抛物线y2=2px的准线,则$-\frac{p}{2}=-1$,求得p的值,求得焦点坐标,代入抛物线方程求得Q点坐标,利用椭圆的定义,即可求得a的值,由b2=a2-c2=8,即可求得椭圆方程;
(Ⅱ)将直线分别代入抛物线,由△=0,求得km=1,将直线方程代入椭圆方程,求得△>0,代入即可求得m的取值范围,切线在x轴上的截距为$x=-\frac{m}{k}$,又$-\frac{m}{k}=-{m^2}>-9$,即可求得切线在x轴上的截距的取值范围.
解答 解:(I)∵抛物线上的点M到y轴的距离等于|MF2|-1,
∴点M到直线x=-1的距离等于点M到焦点F2的距离,---------------(1分)
得x=-1是抛物线y2=2px的准线,即$-\frac{p}{2}=-1$,
解得:p=2,
∴抛物线的方程为y2=4x;-----------------------------------(3分)
可知椭圆的右焦点F2(1,0),左焦点F1(-1,0),
由抛物线的定义及$|Q{F_2}|=\frac{5}{2}$,得${x_Q}+1=\frac{5}{2}$,
又${y_Q}^2=4{x_Q}$,解得:$Q(\frac{3}{2},\;±\sqrt{6})$,-----------------------------------(4分)
由椭圆的定义得2a=|QF1|+|QF2|=$\frac{7}{2}+\frac{5}{2}=6$,----------------------(5分)
∴a=3,又c=1,得b2=a2-c2=8,
∴椭圆的方程为$\frac{x^2}{9}+\frac{y^2}{8}=1$.-------------------------------------------------(6分)
( II)显然k≠0,m≠0,
由$\left\{{\begin{array}{l}{y=kx+m}\\{{y^2}=4x}\end{array}}\right.$,消去x,得ky2-4y+4m=0,
由题意知△1=16-16km=0,得km=1,-----------------------------------(7分)
由$\left\{{\begin{array}{l}{y=kx+m}\\{\frac{x^2}{9}+\frac{y^2}{8}=1}\end{array}}\right.$,消去y,得(9k2+8)x2+18kmx+9m2-72=0,
其中${△_2}={(18km)^2}-4$(9k2+8)(9m2-72)>0,
化简得9k2-m2+8>0,-------------------------------------------------------(9分)
又$k=\frac{1}{m}$,得m4-8m2-9<0,解得0<m2<9,--------------------(10分)
切线在x轴上的截距为$x=-\frac{m}{k}$,又$-\frac{m}{k}=-{m^2}>-9$,
∴切线在x轴上的截距的取值范围是(-9,0).----------------------------------(12分)
点评 本题考查椭圆及抛物线的标准方程及简单几何性质,直线与抛物线及椭圆的位置关系,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-2,1) | C. | $(\frac{1}{2},2)$ | D. | $(\frac{1}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
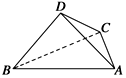 如图所示,四面体ABCD中,已知平面BCD⊥平面ABC,BD⊥DC,BC=6,AB=4$\sqrt{3}$,∠ABC=30°.
如图所示,四面体ABCD中,已知平面BCD⊥平面ABC,BD⊥DC,BC=6,AB=4$\sqrt{3}$,∠ABC=30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{9}{4}]$ | B. | $[\frac{7}{4},+∞)$ | C. | $[\frac{7}{4},\frac{9}{4}]$ | D. | $(-∞,\frac{7}{4}]∪$$[\frac{9}{4},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -1 | C. | -2 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{{\sqrt{2}}}{2}$ | B. | ±1 | C. | $±\frac{{\sqrt{6}}}{3}$ | D. | $±\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com