
| A. | $(-∞,\frac{9}{4}]$ | B. | $[\frac{7}{4},+∞)$ | C. | $[\frac{7}{4},\frac{9}{4}]$ | D. | $(-∞,\frac{7}{4}]∪$$[\frac{9}{4},+∞)$ |
分析 对任意的x1、x2∈R,都有f(x1)≤g(x2)?f(x)max≤g(x)min,分别求出最值即可得出.
解答 解:对任意的x1、x2∈R,都有f(x1)≤g(x2)?f(x)max≤g(x)min,
注意到$f{(x)_{max}}=f(1)=-\frac{1}{4}$,又g(x)=|A-2|sinx≥-|A-2|,
故$-|A-2|≥-\frac{1}{4}⇒|A-2|≤\frac{1}{4}⇒\frac{7}{4}≤A≤\frac{9}{4}$.
故选:C.
点评 本题考查了函数的单调性、等价转化方法、不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:选择题
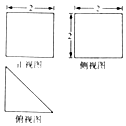 在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的四面体称为鳖臑,某几何体τ的三视图如图所示,将该几何体分别沿棱和表面的对角线截开可得到到一个鳖臑和一个阳马,设V表示体积,则Vτ的外接球:V阳马:V鳖臑=( )
在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的四面体称为鳖臑,某几何体τ的三视图如图所示,将该几何体分别沿棱和表面的对角线截开可得到到一个鳖臑和一个阳马,设V表示体积,则Vτ的外接球:V阳马:V鳖臑=( )| A. | 9π:2:1 | B. | 3$\sqrt{3}$π:3:1 | C. | 3$\sqrt{3}$π:2:1 | D. | 3$\sqrt{3}$π:1:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0} | C. | (-1,1) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2017}$ | B. | $\frac{2π}{2017}$ | C. | $\frac{4π}{2017}$ | D. | $\frac{π}{4034}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com