【题目】《九章算术》里有一段叙述：今有良马与驽马发长安至齐，齐去长安一千一百二十五里，良马初日行一百零三里，日增十三里；驽马初日行九十七里，日减半里；良马先至齐，复还迎驽马，二马相逢.根据该问题设计程序框图如下，若输入
，则输出
的值是（ ）
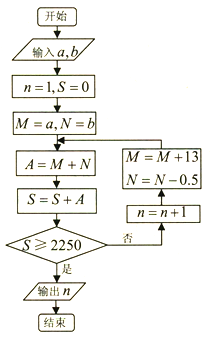
A. 8 B. 9 C. 12 D. 16
科目：高中数学 来源： 题型：
【题目】某品牌汽车的
店，对最近100份分期付款购车情况进行统计，统计情况如下表所示.已知分9期付款的频率为0.4；该店经销一辆该品牌汽车，若顾客分3期付款，其利润为1万元；分6期或9期付款，其利润为2万元；分12期付款，其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
（1）若以上表计算出的频率近似替代概率，从该店采用分期付款购车的顾客（数量较大）中随机抽取3为顾客，求事件
：“至多有1位采用分6期付款“的概率
；
（2）按分层抽样方式从这100为顾客中抽取5人，再从抽取的5人中随机抽取3人，记该店在这3人身上赚取的总利润为随机变量
，求
的分布列和数学期望
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校高二年级举办了一次数学史知识竞赛活动，共有
名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为
分）进行统计，统计结果见下表．请你根据频率分布表解答下列问题：
（1）填出频率分布表中的空格；
（2）为鼓励更多的学生了解“数学史”知识，成绩不低于
分的同学能获奖，请估计在参加的名学生中大概有多少名学生获奖？
（3）在上述统计数据的分析中有一项计算见算法流程图，求输出的
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，直线
经过点
，其倾斜角为
，以原点
为极点，以
轴为非负半轴为极轴，与坐标系取相同的长度单位，建立极坐标系.设曲线
的极坐标方程为
.
（1）若直线与曲线有公共点，求倾斜角的取值范围；
（2）设
为曲线上任意一点，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校有高三文科学生1000人，统计其高三上期期中考试的数学成绩，得到频率分布直方图如下：
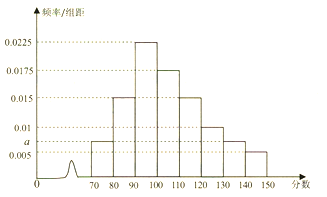
（1）求出图中
的值，并估计本次考试低于120分的人数；
（2）假设同组的每个数据可用该组区间的中点值代替，试估计本次考试不低于120分的同学的平均数（其结果保留一位小数）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出以下命题：
①双曲线
的渐近线方程为y＝±
x；
②命题p：“x∈R，sinx＋
≥2”是真命题；
③已知线性回归方程为
＝3＋2x，当变量x增加2个单位，其预报值平均增加4个单位；
④设随机变量ξ服从正态分布N(0,1)，若P(ξ>1)＝0.2，则P(－1<ξ<0)＝0.6；
⑤设
，则
则正确命题的序号为________(写出所有正确命题的序号)．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
