
ΓΨΧβΡΩΓΩΡ≥¥σ–Ά”ιά÷≥Γ”–ΝΫ÷÷–ΆΚ≈ΒΡΥ°…œΡΠΆ–Θ§Ιήάμ»Υ‘±ΈΣΝΥΝΥΫβΥ°…œΡΠΆ–ΒΡ Ι”Ο«ιΩωΦΑΗχ”ιά÷≥«¥χά¥ΒΡΨ≠ΦΟ ’»κ«ιΩωΘ§Ε‘ΗΟ≥ΓΥυΉνΫϋ6ΡξΥ°…œΡΠΆ–ΒΡ Ι”Ο«ιΩωΫχ––ΝΥΆ≥ΦΤΘ§ΒΟΒΫœύΙΊ ΐΨί»γœ¬±μΘΚ
ΡξΖί | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
ΡξΖί¥ζ¬κx | 1 | 2 | 3 | 4 | 5 | 6 |
Ι”Ο¬ | 11 | 13 | 16 | 15 | 20 | 21 |
Θ®ΔώΘ©«κΗυΨί“‘…œ ΐΨίΘ§”ΟΉν–ΓΕΰ≥ΥΖ®«σΥ°…œΡΠΆ– Ι”Ο¬ ![]() ΙΊ”ΎΡξΖί¥ζ¬κ
ΙΊ”ΎΡξΖί¥ζ¬κ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ§≤Δ‘Λ≤βΗΟ”ιά÷≥Γ2019ΡξΥ°…œΡΠΆ–ΒΡ Ι”Ο¬ ΘΜ
ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ§≤Δ‘Λ≤βΗΟ”ιά÷≥Γ2019ΡξΥ°…œΡΠΆ–ΒΡ Ι”Ο¬ ΘΜ
Θ®ΔρΘ©ΥφΉ≈…ζΜνΥ°ΤΫΒΡΧαΗΏΘ§Άβ≥ω¬Ο”ΈΒΡάœΑΌ–’‘Ϋά¥‘ΫΕύΘ§ΗΟ”ιά÷≥ΓΗυΨίΉ‘…μΖΔ’Ι–η«σΘ§ΉΦ±Η÷Ί–¬ΫχΙΚ“Μ≈ζΥ°…œΡΠΆ–Θ§Τδ–ΆΚ≈÷ς“Σ «ΡΩ«Α Ι”ΟΒΡΔώ–ΆΓΔΔρ–ΆΝΫ÷÷Θ§ΟΩΝΨΦέΗώΖ÷±πΈΣ1Άρ‘ΣΓΔ![]() Άρ‘Σ.ΗυΨί“‘ΆυΨ≠―ιΘ§ΟΩΝΨΥ°…œΡΠΆ–ΒΡΒΡ Ι”ΟΡξœό≤Μ≥§ΙΐΥΡΡξ.”ιά÷≥ΓΙήάμ≤ΩΕ‘“―Ψ≠Χ‘Χ≠ΒΡΝΫΩνΥ°…œΡΠΆ–ΒΡ Ι”Ο«ιΩωΖ÷±π≥ι»ΓΝΥ50ΝΨΫχ––Ά≥ΦΤΘ§ Ι”ΟΡξœό»γΧθ–ΈΆΦΥυ ΨΘΚ
Άρ‘Σ.ΗυΨί“‘ΆυΨ≠―ιΘ§ΟΩΝΨΥ°…œΡΠΆ–ΒΡΒΡ Ι”ΟΡξœό≤Μ≥§ΙΐΥΡΡξ.”ιά÷≥ΓΙήάμ≤ΩΕ‘“―Ψ≠Χ‘Χ≠ΒΡΝΫΩνΥ°…œΡΠΆ–ΒΡ Ι”Ο«ιΩωΖ÷±π≥ι»ΓΝΥ50ΝΨΫχ––Ά≥ΦΤΘ§ Ι”ΟΡξœό»γΧθ–ΈΆΦΥυ ΨΘΚ
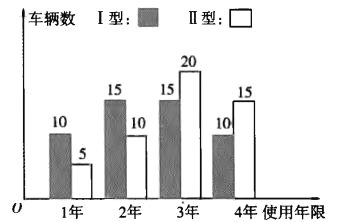
“―÷ΣΟΩΝΨΥ°…œΡΠΆ–¥”ΙΚ»κΒΫΧ‘Χ≠ΤΫΨυΡξ ’“φ «![]() Άρ‘ΣΘ§»τ”ΟΤΒ¬ ΉςΈΣΗ≈¬ Θ§“‘ΟΩΝΨΥ°…œΡΠΆ–¥Ωάϊ»σΘ®¥Ωάϊ»σ= ’“φ-ΙΚ¬ρ≥…±ΨΘ©ΒΡΤΎΆϊ÷ΒΈΣ≤ΈΩΦ÷ΒΘ§‘ρΗΟ”ιά÷≥ΓΒΡΗΚ‘π»Υ”Π―ΓΡΡ÷÷–ΆΚ≈ΒΡΥ°…œΡΠΆ–ΘΩ
Άρ‘ΣΘ§»τ”ΟΤΒ¬ ΉςΈΣΗ≈¬ Θ§“‘ΟΩΝΨΥ°…œΡΠΆ–¥Ωάϊ»σΘ®¥Ωάϊ»σ= ’“φ-ΙΚ¬ρ≥…±ΨΘ©ΒΡΤΎΆϊ÷ΒΈΣ≤ΈΩΦ÷ΒΘ§‘ρΗΟ”ιά÷≥ΓΒΡΗΚ‘π»Υ”Π―ΓΡΡ÷÷–ΆΚ≈ΒΡΥ°…œΡΠΆ–ΘΩ
ΗΫΘΚœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ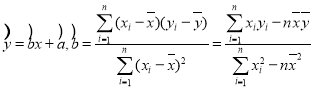 Θ§
Θ§![]() Θ§
Θ§
≤ΈΩΦ ΐΨίΘΚ![]()
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©![]() Θ§ Ι”Ο¬ ΈΣ
Θ§ Ι”Ο¬ ΈΣ![]() .Θ®ΔρΘ©”Π―ΓΙΚΔρ–ΆΚ≈ΒΡΥ°…œΡΠΆ–.
.Θ®ΔρΘ©”Π―ΓΙΚΔρ–ΆΚ≈ΒΡΥ°…œΡΠΆ–.
ΓΨΫβΈωΓΩ
(Δώ)ΗυΨίΙΪ Ϋ÷±Ϋ”ΦΤΥψΦ¥Ω….
(Δρ)Ζ÷±πΦΤΥψΝΫ÷÷–ΆΚ≈ΒΡΥ°…œΡΠΆ– Ι”ΟΡξœόΒΡΗ≈¬ ,‘ΌΖ÷±πΦΤΥψάϊ»σΒΡ ΐ―ßΤΎΆϊ≈–ΕœΦ¥Ω….
ΫβΘΚΘ®ΔώΘ©”…±μΗώ ΐΨίΩ…ΒΟ,![]()
![]()
Υυ“‘Υ°…œΡΠΆ– Ι”Ο¬ ![]() ΙΊ”ΎΡξΖί¥ζ¬κ
ΙΊ”ΎΡξΖί¥ζ¬κ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥Χ «
ΒΡœΏ–‘ΜΊΙιΖΫ≥Χ «![]()
Β±![]() ±,
±,![]() Ι ‘Λ≤βΗΟ”ιά÷≥Γ2019ΡξΥ°…œΡΠΆ–ΒΡ Ι”Ο¬ ΈΣ
Ι ‘Λ≤βΗΟ”ιά÷≥Γ2019ΡξΥ°…œΡΠΆ–ΒΡ Ι”Ο¬ ΈΣ![]() .
.
Θ®ΔρΘ©”…ΤΒ¬ ΉςΗ≈¬ ,ΫαΚœΧθ–ΈΆΦ÷ΣΔώ–ΆΥ°…œΡΠΆ–ΟΩΝΨΩ… Ι”Ο1ΡξΓΔ2ΡξΓΔ3ΡξΚΆ4ΡξΒΡΗ≈¬ Ζ÷±πΈΣ![]() .
.
Υυ“‘ΟΩΝΨΔώ–ΆΥ°…œΡΠΆ–Ω…≤ζ…ζΒΡ¥Ωάϊ»σΒΡΤΎΆϊ÷ΒΈΣΘΚ
![]() Θ®Άρ‘ΣΘ©.
Θ®Άρ‘ΣΘ©.
”…ΤΒ¬ ΉςΗ≈¬ ,ΫαΚœΧθ–ΈΆΦ÷ΣΔρ–ΆΥ°…œΡΠΆ–ΟΩΝΨΩ… Ι”Ο1ΡξΓΔ2ΡξΓΔ3ΡξΚΆ4ΡξΒΡΗ≈¬ Ζ÷±πΈΣ![]() .
.
Υυ“‘ΟΩΝΨΔρ–ΆΥ°…œΡΠΆ–Ω…≤ζ…ζΒΡ¥Ωάϊ»σΒΡΤΎΆϊ÷ΒΈΣΘΚ
![]() Θ®Άρ‘ΣΘ©.
Θ®Άρ‘ΣΘ©.
![]() ,Υυ“‘”Π―ΓΙΚΔρ–ΆΚ≈ΒΡΥ°…œΡΠΆ–.
,Υυ“‘”Π―ΓΙΚΔρ–ΆΚ≈ΒΡΥ°…œΡΠΆ–.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΝΫΉυΫ®÷ΰΈοABΘ§CDΒΡΒΉ≤ΩΕΦ‘ΎΆ§“ΜΗωΥ°ΤΫΟφ…œΘ§«“Ψυ”κΥ°ΤΫΟφ¥Ι÷±Θ§ΥϋΟ«ΒΡΗΏΕ»Ζ÷±π «10mΚΆ20mΘ§¥”Ϋ®÷ΰΈοABΒΡΕΞ≤ΩAΩ¥Ϋ®÷ΰΈοCDΒΡ ”Ϋ«ΓœCADΘΫ60ΓψΘ°
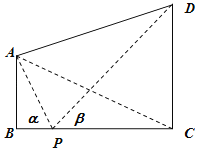
Θ®1Θ©«σBCΒΡ≥ΛΕ»ΘΜ
Θ®2Θ©‘ΎœΏΕΈBC…œ»Γ“ΜΒψPΘ®ΒψP”κΒψBΘ§C≤Μ÷ΊΚœΘ©Θ§¥”ΒψPΩ¥’βΝΫΉυΫ®÷ΰΈοΒΡ ”Ϋ«Ζ÷±πΈΣΓœAPBΘΫΠΝΘ§ΓœDPCΘΫΠ¬Θ§Έ ΒψP‘ΎΚΈ¥Π ±Θ§ΠΝ+Π¬Ήν–ΓΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΑ¬ΉΕΊ―έΓ±Ήχ¬δ‘Ύ”ΔΙζ¬ΉΕΊΧ©Έν ΩΚ”≈œΘ§ « άΫγ…œ ΉΉυΙέΨΑΡΠΧλ¬÷Θ§”÷≥ΤΓΑ«ßλϊ÷°¬÷Γ±Θ§ΗΟΡΠΧλ¬÷ΒΡΑκΨΕΈΣ6Θ®ΒΞΈΜΘΚ![]() Θ©Θ§”ΈΩΆ‘Ύ≥ΥΉχ≤’
Θ©Θ§”ΈΩΆ‘Ύ≥ΥΉχ≤’![]() …ΐΒΫ…œΑκΩ’ΡώνΪ¬ΉΕΊΫ®÷ΰ
…ΐΒΫ…œΑκΩ’ΡώνΪ¬ΉΕΊΫ®÷ΰ![]() Θ§¬ΉΕΊ―έ”κΫ®÷ΰ÷°ΦδΒΡΨύάκ
Θ§¬ΉΕΊ―έ”κΫ®÷ΰ÷°ΦδΒΡΨύάκ![]() ΈΣ12Θ®ΒΞΈΜΘΚ
ΈΣ12Θ®ΒΞΈΜΘΚ![]() Θ©Θ§”ΈΩΆ‘Ύ≥ΥΉχ≤’
Θ©Θ§”ΈΩΆ‘Ύ≥ΥΉχ≤’![]() Ω¥Ϋ®÷ΰ
Ω¥Ϋ®÷ΰ![]() ΒΡ ”Ϋ«ΈΣ
ΒΡ ”Ϋ«ΈΣ![]() .
.

Θ®1Θ©Β±≥ΥΉχ≤’![]() ‘Ύ¬ΉΕΊ―έΒΡΉνΗΏΒψ
‘Ύ¬ΉΕΊ―έΒΡΉνΗΏΒψ![]() ±Θ§ ”Ϋ«
±Θ§ ”Ϋ«![]() Θ§«σΫ®÷ΰ
Θ§«σΫ®÷ΰ![]() ΒΡΗΏΕ»ΘΜ
ΒΡΗΏΕ»ΘΜ
Θ®2Θ©Β±”ΈΩΆ‘Ύ≥ΥΉχ≤’![]() Ω¥Ϋ®÷ΰ
Ω¥Ϋ®÷ΰ![]() ΒΡ ”Ϋ«
ΒΡ ”Ϋ«![]() ΈΣ
ΈΣ![]() ±Θ§≈Ρ…ψ–ßΙϊΉνΚΟ.»τ‘Ύ¬ΉΕΊ―έ…œΩ…“‘≈Ρ…ψΒΫ–ßΙϊΉνΚΟΒΡ’’Τ§Θ§«σΫ®÷ΰ
±Θ§≈Ρ…ψ–ßΙϊΉνΚΟ.»τ‘Ύ¬ΉΕΊ―έ…œΩ…“‘≈Ρ…ψΒΫ–ßΙϊΉνΚΟΒΡ’’Τ§Θ§«σΫ®÷ΰ![]() ΒΡΉνΒΆΗΏΕ».
ΒΡΉνΒΆΗΏΕ».
Θ®ΥΒΟςΘΚΈΣΝΥ±ψ”ΎΦΤΥψΘ§ ΐΨί”κ ΒΦ Ψύάκ”–Έσ≤νΘ§¬ΉΕΊ―έΒΡ ΒΦ ΗΏΕ»ΈΣ![]() Θ©
Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΆχΒξΨ≠œζΡ≥…ΧΤΖΘ§ΈΣΝΥΫβΗΟ…ΧΤΖΒΡ‘¬œζΝΩyΘ®ΒΞΈΜΘΚ«ßΦΰΘ©”κ έΦέxΘ®ΒΞΈΜΘΚ‘Σ/ΦΰΘ©÷°ΦδΒΡΙΊœΒΘ§ ’Φ·5Ήι ΐΨίΫχ––ΝΥ≥θ≤Ϋ¥ΠάμΘ§ΒΟΒΫ»γœ¬ ΐ±μΘΚ
x | 5 | 6 | 7 | 8 | 9 |
y | 8 | 6 | 4.5 | 3.5 | 3 |
Θ®1Θ©Ά≥ΦΤ―ß÷–”ΟœύΙΊœΒ ΐrά¥ΚβΝΩΝΫΗω±δΝΩ÷°ΦδœΏ–‘œύΙΊΙΊœΒΒΡ«Ω»θΘ§»τ![]() Θ§‘ρ»œΈΣœύΙΊ–‘Κή«ΩΘΜ»τ
Θ§‘ρ»œΈΣœύΙΊ–‘Κή«ΩΘΜ»τ![]() Θ§‘ρ»œΈΣœύΙΊ–‘“ΜΑψΘΜ»τ
Θ§‘ρ»œΈΣœύΙΊ–‘“ΜΑψΘΜ»τ![]() Θ§‘ρ»œΈΣœύΙΊ–‘Ϋœ»θ.«κΗυΨί…œ±μ ΐΨίΦΤΥψy”κx÷°ΦδœύΙΊœΒ ΐrΘ§≤ΔΥΒΟςy”κx÷°ΦδΒΡœΏ–‘œύΙΊΙΊœΒΒΡ«Ω»θΘ®ΨΪ»ΖΒΫ0.01Θ©ΘΜ
Θ§‘ρ»œΈΣœύΙΊ–‘Ϋœ»θ.«κΗυΨί…œ±μ ΐΨίΦΤΥψy”κx÷°ΦδœύΙΊœΒ ΐrΘ§≤ΔΥΒΟςy”κx÷°ΦδΒΡœΏ–‘œύΙΊΙΊœΒΒΡ«Ω»θΘ®ΨΪ»ΖΒΫ0.01Θ©ΘΜ
Θ®2Θ©«σyΙΊ”ΎxΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘΜ
Θ®3Θ©ΗυΨίΘ®2Θ©÷–ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ§”ΠΫΪ έΦέxΕ®ΈΣΕύ…ΌΘ§Ω…Μώ»ΓΉν¥σΒΡ‘¬œζ έΫπΕνΘΩΘ®‘¬œζ έΫπΕνΘΫ‘¬œζ έΝΩΓΝΒ±‘¬ έΦέΘ©
ΗΫΉΔΘΚ
≤ΈΩΦ ΐΨίΘΚ![]() Θ§
Θ§
≤ΈΩΦΙΪ ΫΘΚœύΙΊœΒ ΐ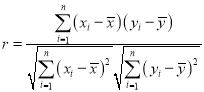 Θ§
Θ§
œΏ–‘ΜΊΙιΖΫ≥Χ![]() Θ§
Θ§ Θ§
Θ§![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2018Ρξ «÷–ΙζΗΡΗοΩΣΖ≈ΒΡΒΎ40÷ήΡξΘ§ΈΣΝΥ≥δΖ÷»œ Ε–¬–Έ Τœ¬ΗΡΗοΩΣΖ≈ΒΡ ±¥ζ–‘Θ§Ρ≥ΒΊΒΡΟώΒςΜζΙΙΥφΜζ―Γ»ΓΝΥΗΟΒΊΒΡ100Οϊ –ΟώΫχ––Βς≤ιΘ§ΫΪΥϊΟ«ΒΡΡξΝδΖ÷≥…6ΕΈΘΚ![]() Θ§≤ΔΜφ÷ΤΝΥ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.
Θ§≤ΔΜφ÷ΤΝΥ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.
Θ®1Θ©œ÷¥”ΡξΝδ‘Ύ![]() ΡΎΒΡ»Υ‘±÷–Α¥Ζ÷≤ψ≥ι―υΒΡΖΫΖ®≥ι»Γ8»ΥΘ§‘Ό¥”’β8»Υ÷–ΥφΜζ≥ι»Γ3»ΥΫχ––ΉυΧΗΘ§”Ο
ΡΎΒΡ»Υ‘±÷–Α¥Ζ÷≤ψ≥ι―υΒΡΖΫΖ®≥ι»Γ8»ΥΘ§‘Ό¥”’β8»Υ÷–ΥφΜζ≥ι»Γ3»ΥΫχ––ΉυΧΗΘ§”Ο![]() ±μ ΨΡξΝδ‘Ύ
±μ ΨΡξΝδ‘Ύ![]() ΡΎΒΡ»Υ ΐΘ§«σ
ΡΎΒΡ»Υ ΐΘ§«σ![]() ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘΜ
ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘΜ
Θ®2Θ©»τ”Ο―υ±ΨΒΡΤΒ¬ ¥ζΧφΗ≈¬ Θ§”ΟΥφΜζ≥ι―υΒΡΖΫΖ®¥”ΗΟΒΊ≥ι»Γ20Οϊ –ΟώΫχ––Βς≤ιΘ§Τδ÷–”–![]() Οϊ –ΟώΒΡΡξΝδ‘Ύ
Οϊ –ΟώΒΡΡξΝδ‘Ύ![]() ΒΡΗ≈¬ ΈΣ
ΒΡΗ≈¬ ΈΣ![]() .Β±
.Β±![]() Ήν¥σ ±Θ§«σ
Ήν¥σ ±Θ§«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒ¬Ιζ÷χΟϊ ΐ―ßΦ“Β“άϊΩΥάΉ(Dirichlet,1805~1859)‘Ύ ΐ―ßΝλ”ρ≥…ΨΆœ‘÷χ.19 άΦΆ,Β“άϊΩΥάΉΕ®“εΝΥ“ΜΗωΓΑΤφΙ÷ΒΡΚ· ΐΓ± 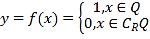 Τδ÷–RΈΣ Β ΐΦ·,QΈΣ”–άμ ΐΦ·.‘ρΙΊ”ΎΚ· ΐ
Τδ÷–RΈΣ Β ΐΦ·,QΈΣ”–άμ ΐΦ·.‘ρΙΊ”ΎΚ· ΐ![]() ”–»γœ¬ΥΡΗωΟϋΧβ,’ΐ»ΖΒΡΈΣ( )
”–»γœ¬ΥΡΗωΟϋΧβ,’ΐ»ΖΒΡΈΣ( )
A.Κ· ΐ![]() «≈ΦΚ· ΐ
«≈ΦΚ· ΐ
B.![]() ,
,![]() ,
,![]() Κψ≥…ΝΔ
Κψ≥…ΝΔ
C.»Έ»Γ“ΜΗω≤ΜΈΣΝψΒΡ”–άμ ΐT,![]() Ε‘»Έ“βΒΡ
Ε‘»Έ“βΒΡ![]() Κψ≥…ΝΔ
Κψ≥…ΝΔ
D.≤Μ¥φ‘Ύ»ΐΗωΒψ![]() ,
,![]() ,
,![]() , ΙΒΟ
, ΙΒΟ![]() ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ
ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΗχΕ®Ά÷‘≤C:![]() (
(![]() ),≥Τ‘≤–Ρ‘Ύ‘≠ΒψO,ΑκΨΕΈΣ
),≥Τ‘≤–Ρ‘Ύ‘≠ΒψO,ΑκΨΕΈΣ![]() ΒΡ‘≤ «Ά÷‘≤CΒΡΓΑΈά–«‘≤Γ±.»τΆ÷‘≤CΒΡάκ–Ρ¬
ΒΡ‘≤ «Ά÷‘≤CΒΡΓΑΈά–«‘≤Γ±.»τΆ÷‘≤CΒΡάκ–Ρ¬ ![]() ,Βψ
,Βψ![]() ‘ΎC…œ.
‘ΎC…œ.
(1)«σΆ÷‘≤CΒΡΖΫ≥ΧΚΆΤδΓΑΈά–«‘≤Γ±ΖΫ≥Χ;
(2)ΒψP «Ά÷‘≤CΒΡΓΑΈά–«‘≤Γ±…œΒΡ“ΜΗωΕ·Βψ,ΙΐΒψPΉς÷±œΏ![]() ,
,![]() ΙΒΟ
ΙΒΟ![]()
![]()
![]() ,”κΆ÷‘≤CΕΦ÷Μ”–“ΜΗωΫΜΒψ,«“
,”κΆ÷‘≤CΕΦ÷Μ”–“ΜΗωΫΜΒψ,«“![]() ,
,![]() Ζ÷±πΫΜΤδΓΑΈά–«‘≤Γ±”ΎΒψM,N,÷ΛΟς:œ“≥Λ
Ζ÷±πΫΜΤδΓΑΈά–«‘≤Γ±”ΎΒψM,N,÷ΛΟς:œ“≥Λ![]() ΈΣΕ®÷Β.
ΈΣΕ®÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤CΘΚ![]() +
+![]() =1Θ®aΘΨbΘΨ0Θ©ΒΡΝΫΗωΫΙΒψΖ÷±πΈΣF1Θ®©¹2Θ§0Θ©Θ§F2Θ®2Θ§0Θ©Θ§άκ–Ρ¬ ΈΣ
=1Θ®aΘΨbΘΨ0Θ©ΒΡΝΫΗωΫΙΒψΖ÷±πΈΣF1Θ®©¹2Θ§0Θ©Θ§F2Θ®2Θ§0Θ©Θ§άκ–Ρ¬ ΈΣ![]() Θ°ΙΐΫΙΒψF2ΒΡ÷±œΏlΘ®–±¬ ≤ΜΈΣ0Θ©”κΆ÷‘≤CΫΜ”ΎAΘ§BΝΫΒψΘ§œΏΕΈABΒΡ÷–ΒψΈΣDΘ§OΈΣΉχ±ξ‘≠ΒψΘ§÷±œΏODΫΜΆ÷‘≤”ΎMΘ§NΝΫΒψΘ°
Θ°ΙΐΫΙΒψF2ΒΡ÷±œΏlΘ®–±¬ ≤ΜΈΣ0Θ©”κΆ÷‘≤CΫΜ”ΎAΘ§BΝΫΒψΘ§œΏΕΈABΒΡ÷–ΒψΈΣDΘ§OΈΣΉχ±ξ‘≠ΒψΘ§÷±œΏODΫΜΆ÷‘≤”ΎMΘ§NΝΫΒψΘ°
Θ®ΔώΘ©«σΆ÷‘≤CΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©Β±ΥΡ±Ώ–ΈMF1NF2ΈΣΨΊ–Έ ±Θ§«σ÷±œΏlΒΡΖΫ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2019Ρξ «÷–ΜΣ»ΥΟώΙ≤ΚΆΙζ≥…ΝΔ70÷ήΡξΘ°ΈΣΝΥ»Ο»ΥΟώΝΥΫβΫ®Ιζ70÷ήΡξΒΡΖγ”ξάζ≥ΧΘ§Ρ≥ΒΊΒΡΟώΒςΜζΙΙΥφΜζ―Γ»ΓΝΥΗΟΒΊΒΡ100Οϊ –ΟώΫχ––Βς≤ιΘ§ΫΪΥϊΟ«ΒΡΡξΝδΖ÷≥…6ΕΈΘΚ![]() Θ§
Θ§![]() Θ§Γ≠Θ§
Θ§Γ≠Θ§![]() Θ§≤ΔΜφ÷ΤΝΥ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ°
Θ§≤ΔΜφ÷ΤΝΥ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ°

Θ®1Θ©œ÷¥”ΡξΝδ‘Ύ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΡΎΒΡ»Υ‘±÷–Α¥Ζ÷≤ψ≥ι―υΒΡΖΫΖ®≥ι»Γ8»ΥΘ§‘Ό¥”’β8»Υ÷–ΥφΜζ―Γ»Γ3»ΥΫχ––ΉυΧΗΘ§”Ο
ΡΎΒΡ»Υ‘±÷–Α¥Ζ÷≤ψ≥ι―υΒΡΖΫΖ®≥ι»Γ8»ΥΘ§‘Ό¥”’β8»Υ÷–ΥφΜζ―Γ»Γ3»ΥΫχ––ΉυΧΗΘ§”Ο![]() ±μ ΨΡξΝδ‘Ύ
±μ ΨΡξΝδ‘Ύ![]() Θ©ΡΎΒΡ»Υ ΐΘ§«σ
Θ©ΡΎΒΡ»Υ ΐΘ§«σ![]() ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘΜ
ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘΜ
Θ®2Θ©»τ”Ο―υ±ΨΒΡΤΒ¬ ¥ζΧφΗ≈¬ Θ§”ΟΥφΜζ≥ι―υΒΡΖΫΖ®¥”ΗΟΒΊ≥ι»Γ20Οϊ –ΟώΫχ––Βς≤ιΘ§Τδ÷–”–![]() Οϊ –ΟώΒΡΡξΝδ‘Ύ
Οϊ –ΟώΒΡΡξΝδ‘Ύ![]() ΒΡΗ≈¬ ΈΣ
ΒΡΗ≈¬ ΈΣ![]() Θ°Β±
Θ°Β±![]() Ήν¥σ ±Θ§«σ
Ήν¥σ ±Θ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com