
【题目】德国著名数学家狄利克雷(Dirichlet,1805~1859)在数学领域成就显著.19世纪,狄利克雷定义了一个“奇怪的函数” 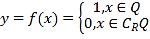 其中R为实数集,Q为有理数集.则关于函数
其中R为实数集,Q为有理数集.则关于函数![]() 有如下四个命题,正确的为( )
有如下四个命题,正确的为( )
A.函数![]() 是偶函数
是偶函数
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一个不为零的有理数T,![]() 对任意的
对任意的![]() 恒成立
恒成立
D.不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
【答案】ACD
【解析】
根据函数的定义以及解析式,逐项判断即可.
对于A,若![]() ,则
,则![]() ,满足
,满足![]() ;若
;若![]() ,则
,则![]() ,满足
,满足![]() ;故函数
;故函数![]() 为偶函数,选项A正确;
为偶函数,选项A正确;
对于B,取![]() ,则
,则![]() ,
,![]() ,故选项B错误;
,故选项B错误;
对于C,若![]() ,则
,则![]() ,满足
,满足![]() ;若
;若![]() ,则
,则![]() ,满足
,满足![]() ,故选项C正确;
,故选项C正确;
对于D,要为等腰直角三角形,只可能如下四种情况:
①直角顶点![]() 在
在![]() 上,斜边在
上,斜边在![]() 轴上,此时点
轴上,此时点![]() ,点
,点![]() 的横坐标为无理数,则
的横坐标为无理数,则![]() 中点的横坐标仍然为无理数,那么点
中点的横坐标仍然为无理数,那么点![]() 的横坐标也为无理数,这与点
的横坐标也为无理数,这与点![]() 的纵坐标为1矛盾,故不成立;
的纵坐标为1矛盾,故不成立;
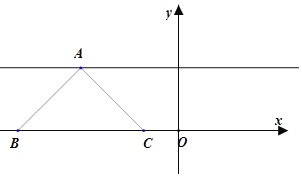
②直角顶点![]() 在
在![]() 上,斜边不在
上,斜边不在![]() 轴上,此时点
轴上,此时点![]() 的横坐标为无理数,则点
的横坐标为无理数,则点![]() 的横坐标也应为无理数,这与点
的横坐标也应为无理数,这与点![]() 的纵坐标为1矛盾,故不成立;
的纵坐标为1矛盾,故不成立;
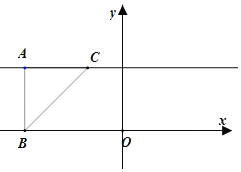
③直角顶点![]() 在
在![]() 轴上,斜边在
轴上,斜边在![]() 上,此时点
上,此时点![]() ,点
,点![]() 的横坐标为有理数,则
的横坐标为有理数,则![]() 中点的横坐标仍然为有理数,那么点
中点的横坐标仍然为有理数,那么点![]() 的横坐标也应为有理数,这与点
的横坐标也应为有理数,这与点![]() 的纵坐标为0矛盾,故不成立;
的纵坐标为0矛盾,故不成立;
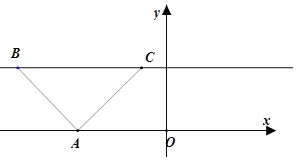
④直角顶点![]() 在
在![]() 轴上,斜边不在
轴上,斜边不在![]() 上,此时点
上,此时点![]() 的横坐标为无理数,则点
的横坐标为无理数,则点![]() 的横坐标也应为无理数,这与点
的横坐标也应为无理数,这与点![]() 的纵坐标为1矛盾,故不成立.
的纵坐标为1矛盾,故不成立.
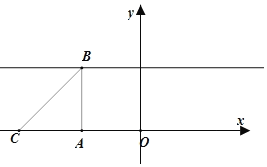
综上,不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等腰直角三角形,故选项D正确.
为等腰直角三角形,故选项D正确.
故选:![]() .
.


科目:高中数学 来源: 题型:
【题目】某车间4小时内生产了100根不同规格的三角钢材(单位:厘米),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.
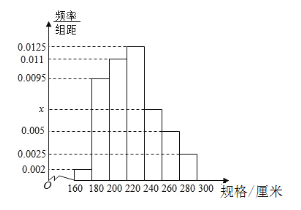
(1)求直方图中![]() 的值;
的值;
(2)求这批钢材规格的众数;
(3)在规格为![]() ,
,![]() ,
,![]() ,
,![]() 的四组钢材中,用分层抽样的方法抽取11根钢材,则在
的四组钢材中,用分层抽样的方法抽取11根钢材,则在![]() 的规格中应抽取多少根?
的规格中应抽取多少根?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校有歌唱和舞蹈两个兴趣小组,其中歌唱组有 4 名男生,1 名女生,舞蹈组有2 名男生,2 名女生,学校计划从两兴趣小组中各选2名同学参加演出.
(1)求选出的4名同学中至多有2名女生的选派方法数;
(2)记X为选出的4名同学中女生的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型娱乐场有两种型号的水上摩托,管理人员为了了解水上摩托的使用情况及给娱乐城带来的经济收入情况,对该场所最近6年水上摩托的使用情况进行了统计,得到相关数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 |
使用率 | 11 | 13 | 16 | 15 | 20 | 21 |
(Ⅰ)请根据以上数据,用最小二乘法求水上摩托使用率![]() 关于年份代码
关于年份代码![]() 的线性回归方程,并预测该娱乐场2019年水上摩托的使用率;
的线性回归方程,并预测该娱乐场2019年水上摩托的使用率;
(Ⅱ)随着生活水平的提高,外出旅游的老百姓越来越多,该娱乐场根据自身发展需求,准备重新进购一批水上摩托,其型号主要是目前使用的Ⅰ型、Ⅱ型两种,每辆价格分别为1万元、![]() 万元.根据以往经验,每辆水上摩托的的使用年限不超过四年.娱乐场管理部对已经淘汰的两款水上摩托的使用情况分别抽取了50辆进行统计,使用年限如条形图所示:
万元.根据以往经验,每辆水上摩托的的使用年限不超过四年.娱乐场管理部对已经淘汰的两款水上摩托的使用情况分别抽取了50辆进行统计,使用年限如条形图所示:
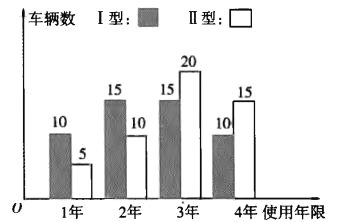
已知每辆水上摩托从购入到淘汰平均年收益是![]() 万元,若用频率作为概率,以每辆水上摩托纯利润(纯利润=收益-购买成本)的期望值为参考值,则该娱乐场的负责人应选哪种型号的水上摩托?
万元,若用频率作为概率,以每辆水上摩托纯利润(纯利润=收益-购买成本)的期望值为参考值,则该娱乐场的负责人应选哪种型号的水上摩托?
附:线性回归方程为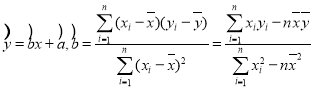 ,
,![]() ,
,
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖膈(bie nao)指四个面均为直角三角形的四面体.如图在堑堵![]() 中,
中,![]() .
.
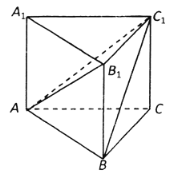
(1)求证:四棱锥![]() 为阳马;
为阳马;
(2)若![]() ,当鳖膈
,当鳖膈![]() 体积最大时,求锐二面角
体积最大时,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“总把新桃换旧符”(王安石)、“灯前小草写桃符”(陆游),春节是中华民族的传统节日,在宋代人们用写“桃符”的方式来祈福避祸,而现代人们通过贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿,某商家在春节前开展商品促销活动,顾客凡购物金额满50元,则可以从“福”字、春联和灯笼这三类礼品中任意免费领取一件,若有4名顾客都领取一件礼品,则他们中有且仅有2人领取的礼品种类相同的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制如图所示频率分布直方图,已知中间三组的人数可构成等差数列.
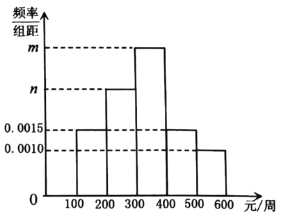
(1)求![]() 的值;
的值;
(2)分析人员对100名调查对象的性别进行统计发现,消费金额不低于300元的男性有20人,低于300元的男性有25人,根据统计数据完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费金额与性别有关?
的把握认为消费金额与性别有关?
(3)分析人员对抽取对象每周的消费金额![]() 与年龄
与年龄![]() 进一步分析,发现他们线性相关,得到回归方程
进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
![]() 列联表
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com