
【题目】某车间4小时内生产了100根不同规格的三角钢材(单位:厘米),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.
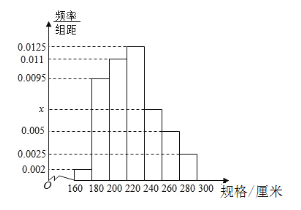
(1)求直方图中![]() 的值;
的值;
(2)求这批钢材规格的众数;
(3)在规格为![]() ,
,![]() ,
,![]() ,
,![]() 的四组钢材中,用分层抽样的方法抽取11根钢材,则在
的四组钢材中,用分层抽样的方法抽取11根钢材,则在![]() 的规格中应抽取多少根?
的规格中应抽取多少根?
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为增强市民交通规范意识,我市面向全市征召劝导员志愿者,分布于各候车亭或十字路口处.现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示.
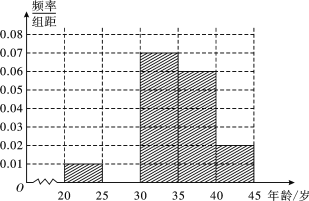
分组(单位:岁) | 频数 | 频率 |
| 5 |
|
| ① |
|
|
| ② |
|
|
|
|
|
|
合计 |
|
|
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数;
(2)在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加“规范摩的司机的交通意识”培训活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=2px(p>0),焦点F到准线的距离为3,抛物线E上的两个动点A(x1,y1)和B(x2,y2),其中x1≠x2且x1+x2=4.线段AB的垂直平分线与x轴交于点 C.
(1)求抛物线E的方程;
(2)求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是10m和20m,从建筑物AB的顶部A看建筑物CD的视角∠CAD=60°.
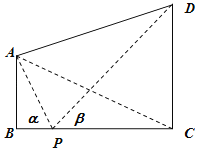
(1)求BC的长度;
(2)在线段BC上取一点P(点P与点B,C不重合),从点P看这两座建筑物的视角分别为∠APB=α,∠DPC=β,问点P在何处时,α+β最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
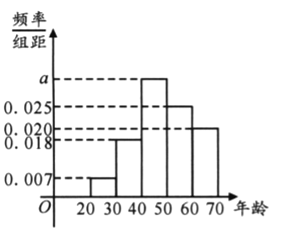
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
名作为样本进行分析,按年龄段![]() 分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
年龄 (单位:岁) |
|
|
|
|
|
保费 (单位:元) |
|
|
|
|
|
(1)用样本的频率分布估计总体分布,为使公司不亏本,求![]() 精确到整数时的最小值
精确到整数时的最小值![]() ;
;
(2![]() 之间的老人每
之间的老人每![]() 人中有
人中有![]() 人患该项疾病(以此频率作为概率).该病的治疗费为
人患该项疾病(以此频率作为概率).该病的治疗费为![]() 元,如果参保,保险公司补贴治疗费
元,如果参保,保险公司补贴治疗费![]() 元.某老人年龄
元.某老人年龄![]() 岁,若购买该项保险(
岁,若购买该项保险(![]() 取
取![]() 中的
中的![]() ).针对此疾病所支付的费用为
).针对此疾病所支付的费用为![]() 元;若没有购买该项保险,针对此疾病所支付的费用为
元;若没有购买该项保险,针对此疾病所支付的费用为![]() 元.试比较
元.试比较![]() 和
和![]() 的期望值大小,并判断该老人购买此项保险是否划算?
的期望值大小,并判断该老人购买此项保险是否划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出己知线段的黄金分割点,具体方法如下:(l)取线段AB=2,过点B作AB的垂线,并用圆规在垂线上截取BC=![]() AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:
AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:![]() 2.236)
2.236)
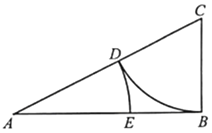
A. 0.236B. 0.382C. 0.472D. 0.618
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷(Dirichlet,1805~1859)在数学领域成就显著.19世纪,狄利克雷定义了一个“奇怪的函数” 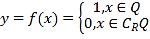 其中R为实数集,Q为有理数集.则关于函数
其中R为实数集,Q为有理数集.则关于函数![]() 有如下四个命题,正确的为( )
有如下四个命题,正确的为( )
A.函数![]() 是偶函数
是偶函数
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一个不为零的有理数T,![]() 对任意的
对任意的![]() 恒成立
恒成立
D.不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com