
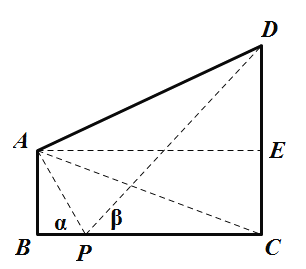
【题目】如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是10m和20m,从建筑物AB的顶部A看建筑物CD的视角∠CAD=60°.
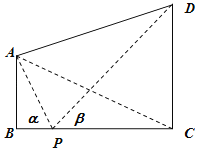
(1)求BC的长度;
(2)在线段BC上取一点P(点P与点B,C不重合),从点P看这两座建筑物的视角分别为∠APB=α,∠DPC=β,问点P在何处时,α+β最小?
【答案】(1)![]() ;(2)当BP为
;(2)当BP为![]() cm时,α+β取得最小值.
cm时,α+β取得最小值.
【解析】
(1)作AE⊥CD,垂足为E,则CE=10,DE=10,设BC=x,根据![]() 得到
得到![]() ,解得答案.
,解得答案.
(2)设BP=t,则![]() ,故
,故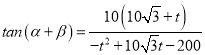 ,设
,设![]() ,求导得到函数单调性,得到最值.
,求导得到函数单调性,得到最值.
(1)作AE⊥CD,垂足为E,则CE=10,DE=10,设BC=x,
则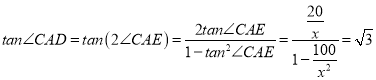 ,
,
化简得![]() ,解之得,
,解之得,![]() 或
或![]() (舍),
(舍),
(2)设BP=t,则![]() ,
,
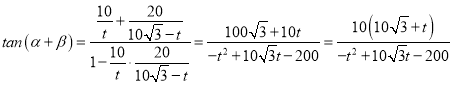 ,
,
设![]() ,
,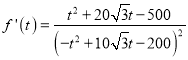 ,
,
令f'(t)=0,因为![]() ,得
,得![]() ,
,
当![]() 时,f'(t)<0,f(t)是减函数;
时,f'(t)<0,f(t)是减函数;
当![]() 时,f'(t)>0,f(t)是增函数,
时,f'(t)>0,f(t)是增函数,
所以,当![]() 时,f(t)取得最小值,即tan(α+β)取得最小值,
时,f(t)取得最小值,即tan(α+β)取得最小值,
因为![]() 恒成立,所以f(t)<0,
恒成立,所以f(t)<0,
所以tan(α+β)<0,![]() ,
,
因为y=tanx在![]() 上是增函数,所以当
上是增函数,所以当![]() 时,α+β取得最小值.
时,α+β取得最小值.


科目:高中数学 来源: 题型:
【题目】某小学六年级学生的进行一分钟跳绳检测,现一班二班各有50人,根据检测结果绘出了一班的频数分布表和二班的频率分布直方图.
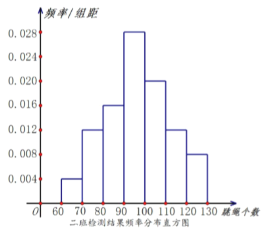
一班检测结果频数分布表:
跳绳个数区间 |
|
|
|
|
|
频数 | 7 | 13 | 20 | 8 | 2 |
(1)根据给出的图表估计一班和二班检测结果的中位数(结果保留两位小数);
(2)跳绳个数不小于100个为优秀,填写下面2×2列联表,并根据列联表判断是否有95%的把握认为检测结果是否优秀与班级有关.
一班 | 二班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式及数据: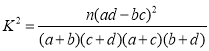 ,
,
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有A,B、C、D四人先后感染了新型冠状病毒,其中只有A到过疫区,B肯定是受A感染的,对于C,因为难以判定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是![]() ,同样也假设D受A、B和C感染的概率都是
,同样也假设D受A、B和C感染的概率都是![]() .在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量,写出X的可能取值为______,并求X的均值(即数学期望)为______.
.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量,写出X的可能取值为______,并求X的均值(即数学期望)为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种赌博每局的规则是:赌客先在标记有1,2,3,4,5的卡片中随机摸取一张,将卡片上的数字作为其赌金;随后放回该卡片,再随机摸取两张,将这两张卡片上数字之差的绝对值的1.4倍作为其奖金.若随机变量ξ1和ξ2分别表示赌客在一局赌博中的赌金和奖金,则D(ξ1)=_____,E(ξ1)﹣E(ξ2)=_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间4小时内生产了100根不同规格的三角钢材(单位:厘米),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.
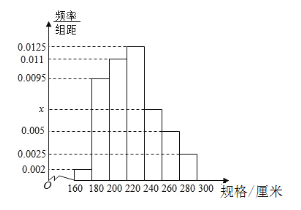
(1)求直方图中![]() 的值;
的值;
(2)求这批钢材规格的众数;
(3)在规格为![]() ,
,![]() ,
,![]() ,
,![]() 的四组钢材中,用分层抽样的方法抽取11根钢材,则在
的四组钢材中,用分层抽样的方法抽取11根钢材,则在![]() 的规格中应抽取多少根?
的规格中应抽取多少根?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中把三角形的田称为“圭田”,把直角梯形的田称为“邪田”,称底是“广”,称高是“正从”,“步”是丈量土地的单位.现有一邪田,广分别为十步和二十步,正从为十步,其内有一块广为八步,正从为五步的圭田.若在邪田内随机种植一株茶树,求该株茶树恰好种在圭田内的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两射线
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两射线![]() 、
、![]() 相互垂直,与曲线C分别相交于A、B两点(不同于点O),且
相互垂直,与曲线C分别相交于A、B两点(不同于点O),且![]() 的倾斜角为锐角
的倾斜角为锐角![]() .
.
(1)求曲线C和射线![]() 的极坐标方程;
的极坐标方程;
(2)求△OAB的面积的最小值,并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型娱乐场有两种型号的水上摩托,管理人员为了了解水上摩托的使用情况及给娱乐城带来的经济收入情况,对该场所最近6年水上摩托的使用情况进行了统计,得到相关数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 |
使用率 | 11 | 13 | 16 | 15 | 20 | 21 |
(Ⅰ)请根据以上数据,用最小二乘法求水上摩托使用率![]() 关于年份代码
关于年份代码![]() 的线性回归方程,并预测该娱乐场2019年水上摩托的使用率;
的线性回归方程,并预测该娱乐场2019年水上摩托的使用率;
(Ⅱ)随着生活水平的提高,外出旅游的老百姓越来越多,该娱乐场根据自身发展需求,准备重新进购一批水上摩托,其型号主要是目前使用的Ⅰ型、Ⅱ型两种,每辆价格分别为1万元、![]() 万元.根据以往经验,每辆水上摩托的的使用年限不超过四年.娱乐场管理部对已经淘汰的两款水上摩托的使用情况分别抽取了50辆进行统计,使用年限如条形图所示:
万元.根据以往经验,每辆水上摩托的的使用年限不超过四年.娱乐场管理部对已经淘汰的两款水上摩托的使用情况分别抽取了50辆进行统计,使用年限如条形图所示:
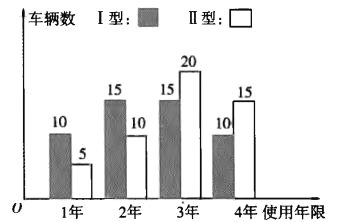
已知每辆水上摩托从购入到淘汰平均年收益是![]() 万元,若用频率作为概率,以每辆水上摩托纯利润(纯利润=收益-购买成本)的期望值为参考值,则该娱乐场的负责人应选哪种型号的水上摩托?
万元,若用频率作为概率,以每辆水上摩托纯利润(纯利润=收益-购买成本)的期望值为参考值,则该娱乐场的负责人应选哪种型号的水上摩托?
附:线性回归方程为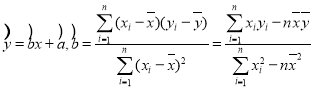 ,
,![]() ,
,
参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com