
【题目】已知四棱锥![]() 中,
中,![]() ,
,![]() .
.
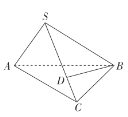
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 是线段
是线段![]() 上靠近
上靠近![]() 的三等分点,求直线
的三等分点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)1.
【解析】
(1)在![]() 中,利用余弦定理,可求得
中,利用余弦定理,可求得![]() ,用勾股定理,可证得
,用勾股定理,可证得![]() ,
,![]() ,继而可证
,继而可证![]() 平面
平面![]() ,即得证;
,即得证;
(2))以![]() 为坐标原点,过点
为坐标原点,过点![]() 作平行于
作平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 作垂直于平面
作垂直于平面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系,分别求解直线
轴,建立空间直角坐标系,分别求解直线![]() 的方向向量,平面
的方向向量,平面![]() 的法向量,利用线面角的向量公式,即得解
的法向量,利用线面角的向量公式,即得解
(1)不妨设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
因为![]() ,由余弦定理,
,由余弦定理,![]() ,解得
,解得![]() ,
,
故![]() ,则
,则![]() ;
;
而![]() ,则
,则![]() ,
,
因为![]() ,故
,故![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点,过点
为坐标原点,过点![]() 作平行于
作平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 作垂直于平面
作垂直于平面![]() 的直线为
的直线为![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
设![]() ,由(1)可知
,由(1)可知![]() ,
,![]()
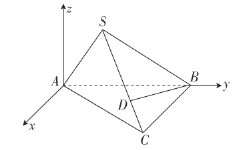
设![]() 点坐标为
点坐标为![]() ,由
,由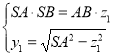 ,
,
解得![]() ,
,![]() ,即
,即![]() 点坐标为
点坐标为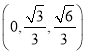 ,
,
设平面![]() 的法向量为
的法向量为![]() ,所以
,所以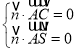 ,
,
所以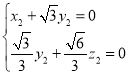 ,令
,令![]() ,得
,得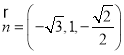 ,
,
而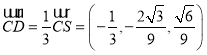 ,故
,故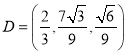 ,故
,故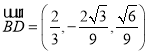 ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则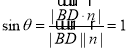 .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】美团外卖和百度外卖两家公司其“骑手”的日工资方案如下:美团外卖规定底薪70元,每单抽成1元;百度外卖规定底薪100元,每日前45单无抽成,超出45单的部分每单抽成6元,假设同一公司的“骑手”一日送餐单数相同,现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数,得到如下条形图:
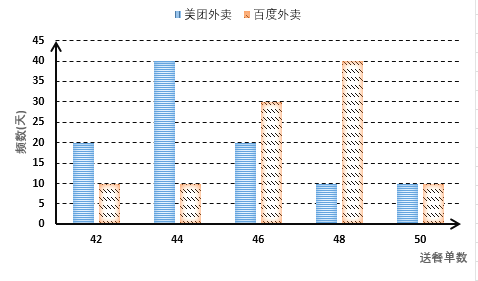
(Ⅰ)求百度外卖公司的“骑手”一日工资![]() (单位:元)与送餐单数
(单位:元)与送餐单数![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
①记百度外卖的“骑手”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小明拟到这两家公司中的一家应聘“骑手”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新型冠状病毒疫情期间,商业活动受到很大影响某小型零售连锁店总部统计了本地区50家加盟店2月份的零售情况,统计数据如图所示.据估计,平均销售收入比去年同期下降40%,则去年2月份这50家加盟店的平均销售收入约为( )
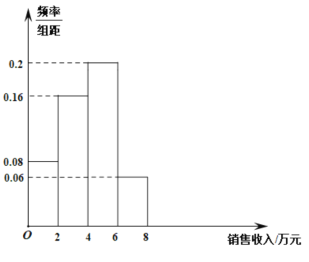
A.6.6万元B.3.96万元C.9.9万元D.7.92万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设你有一笔资金,现有三种投资方案,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
现打算投资10天,三种投资方案的总收益分别为![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点S( -2,0) ,T(2,0),动点P为平面上一个动点,且直线SP、TP的斜率之积为![]() .
.
(1)求动点P的轨迹E的方程;
(2)设点B为轨迹E与y轴正半轴的交点,是否存在直线l,使得l交轨迹E于M,N两点,且F(1,0)恰是△BMN的垂心?若存在,求l的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com