
【题目】已知函数![]() .
.
(1)若![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(2)若![]() ,且函数
,且函数![]() 的值域为
的值域为![]() ,求
,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《 环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过
的年平均浓度不得超过![]() 微克/立方米,
微克/立方米,![]() 的
的![]() 小时平均浓度不得超过
小时平均浓度不得超过![]() 微克/立方米.我市环保局随机抽取了一居民区
微克/立方米.我市环保局随机抽取了一居民区![]() 年
年![]() 天
天![]() 的
的![]() 小时平均浓度(单位:微克/立方米)的监测数据,数据统计如下表:
小时平均浓度(单位:微克/立方米)的监测数据,数据统计如下表:
组别 |
| 频数(天) | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
(1)这![]() 天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.
天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.

①求图中![]() 的值;
的值;
②求样本平均数,并根据样本估计总体的思想,从![]() 的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由;
的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由;
(2)将频率视为概率,对于![]() 年的某
年的某![]() 天,记这
天,记这![]() 天中该居民区
天中该居民区![]() 的
的![]() 小时平均浓度符合环境空气质量标准的天数为
小时平均浓度符合环境空气质量标准的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠DAB=60°,AD⊥PD,点F为棱PD的中点.
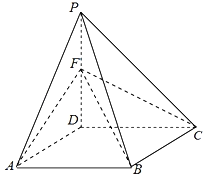
(1)在棱BC上是否存在一点E,使得CF∥平面PAE,并说明理由;
(2)若AC⊥PB,二面角D﹣FC﹣B的余弦值为![]() 时,求直线AF与平面BCF所成的角的正弦值.
时,求直线AF与平面BCF所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点
于点![]() ,交棱
,交棱![]() 于点
于点![]() ,下列正确的是( )
,下列正确的是( )
A.平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
B.四边形![]() 一定是平行四边形;
一定是平行四边形;
C.平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
D.四边形![]() 的面积有最大值.
的面积有最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知0<m<2,动点M到两定点F1(﹣m,0),F2(m,0)的距离之和为4,设点M的轨迹为曲线C,若曲线C过点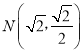 .
.
(1)求m的值以及曲线C的方程;
(2)过定点![]() 且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】政府工作报告指出,2019年我国深入实施创新驱动发展战略,创新能力和效率进一步提升;2020年要提升科技支撑能力,健全以企业为主体的产学研一体化创新机制,某企业为了提升行业核心竞争力,逐渐加大了科技投入;该企业连续5年来的科技投入x(百万元)与收益y(百万元)的数据统计如下:
科技投入x | 1 | 2 | 3 | 4 | 5 |
收益y | 40 | 50 | 60 | 70 | 90 |
(1)请根据表中数据,建立y关于x的线性回归方程;
(2)按照(1)中模型,已知科技投入8百万元时收益为140百万元,求残差![]() (残差
(残差![]() 真实值-预报值).
真实值-预报值).
参考数据:回归直线方程![]() ,其中
,其中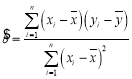 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com