
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 在区间
在区间![]() 上存在两个不同零点,求实数
上存在两个不同零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2)![]() .
.
【解析】
试题分析:(1)先求导数,再根据a讨论导函数零点,根据导函数零点情况讨论导函数符号,根据导函数符号确定函数单调性,(2)先分离![]() ,再利用导数研究函数
,再利用导数研究函数![]() 单调性,最后根据图像确定存在两个不同零点的条件,解对应不等式得实数
单调性,最后根据图像确定存在两个不同零点的条件,解对应不等式得实数![]() 的取值范围.
的取值范围.
试题解析:(1)∵![]()
①若![]() 时,
时,![]() ,此时函数在
,此时函数在![]() 上单调递增;
上单调递增;
②若![]() 时,又
时,又![]() 得:
得:![]()
![]() 时
时![]() ,此时函数在
,此时函数在![]() 上单调递减;
上单调递减;
当![]() 时
时![]() ,此时函数在
,此时函数在![]() 上单调递增;
上单调递增;
(2)由题意知:![]() 在区间
在区间![]() 上有两个不同实数解,
上有两个不同实数解,
即函数![]() 图像与函数
图像与函数![]() 图像有两个不同的交点,
图像有两个不同的交点,
因为![]() ,令
,令![]() 得:
得:![]()
所以当![]() 时,
时,![]() ,函数在
,函数在![]() 上单调递减
上单调递减
当![]() 时,
时,![]() ,函数在
,函数在![]() 上单调递增;
上单调递增;
则![]() ,而
,而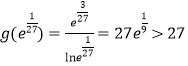 ,且
,且![]() ,
,
要使函数![]() 图像与函数
图像与函数![]() 图像有两个不同的交点,
图像有两个不同的交点,
所以![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上![]() 至
至![]() 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为![]() ,
,![]() ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点S( -2,0) ,T(2,0),动点P为平面上一个动点,且直线SP、TP的斜率之积为![]() .
.
(1)求动点P的轨迹E的方程;
(2)设点B为轨迹E与y轴正半轴的交点,是否存在直线l,使得l交轨迹E于M,N两点,且F(1,0)恰是△BMN的垂心?若存在,求l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图,下列描述正确的是( ).
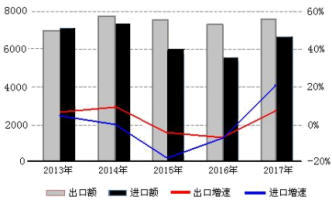
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
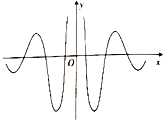
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,其右焦点F到其右准线的距离为1,离心率为
,其右焦点F到其右准线的距离为1,离心率为![]() ,A,B分别为椭圆
,A,B分别为椭圆![]() 的上、下顶点,过点F且不与x轴重合的直线l与椭圆
的上、下顶点,过点F且不与x轴重合的直线l与椭圆![]() 交于C,D两点,与y轴交于点P,直线
交于C,D两点,与y轴交于点P,直线![]() 与
与![]() 交于点Q.
交于点Q.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )

A.20°B.40°
C.50°D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com