
【题目】已知函数![]() ,
,![]() 为
为![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,
时,
(i)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(ii)求函数![]() 的单调区间和极值;
的单调区间和极值;
(Ⅱ)当![]() 时,求证:对任意的
时,求证:对任意的![]() ,且
,且![]() ,有
,有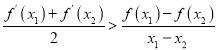 .
.
【答案】(Ⅰ)(i)![]() ;(ii)
;(ii)![]() 的极小值为
的极小值为![]() ,无极大值;(Ⅱ)证明见解析.
,无极大值;(Ⅱ)证明见解析.
【解析】
(Ⅰ) (i)首先求得导函数的解析式,然后结合导数的几何意义求解切线方程即可;
(ii)首先求得![]() 的解析式,然后利用导函数与原函数的关系讨论函数的单调性和函数的极值即可;
的解析式,然后利用导函数与原函数的关系讨论函数的单调性和函数的极值即可;
(Ⅱ)首先确定导函数的解析式,然后令![]() ,将原问题转化为与
,将原问题转化为与![]() 有关的函数,然后构造新函数,利用新函数的性质即可证得题中的结论.
有关的函数,然后构造新函数,利用新函数的性质即可证得题中的结论.
(Ⅰ) (i) 当k=6时,![]() ,
,![]() .可得
.可得![]() ,
,![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(ii) 依题意,![]() .
.
从而可得![]() ,
,
整理可得:![]() ,
,
令![]() ,解得
,解得![]() .
.
当x变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
所以,函数g(x)的单调递减区间为(0,1),单调递增区间为(1,+∞);
g(x)的极小值为g(1)=1,无极大值.
(Ⅱ)证明:由![]() ,得
,得![]() .
.
对任意的![]() ,且
,且![]() ,令
,令![]() ,则
,则
![]()
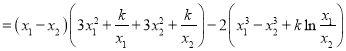
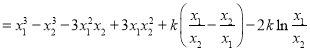
![]() . ①
. ①
令![]() .
.
当x>1时,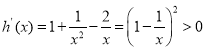 ,
,
由此可得![]() 在
在![]() 单调递增,所以当t>1时,
单调递增,所以当t>1时,![]() ,即
,即![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]()
![]() . ②
. ②
由(Ⅰ)(ii)可知,当![]() 时,
时,![]() ,即
,即![]() ,
,
故![]() ③
③
由①②③可得![]() .
.
所以,当![]() 时,任意的
时,任意的![]() ,且
,且![]() ,有
,有
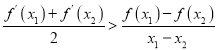 .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]()
![]() ,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
在△![]() 中,内角A,B,C所对的边分别为
中,内角A,B,C所对的边分别为![]() .且满足_________.
.且满足_________.
(1)求![]() ;
;
(2)已知![]() ,△
,△![]() 的外接圆半径为
的外接圆半径为![]() ,求△
,求△![]() 的边AB上的高
的边AB上的高![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为加强对销售员的考核与管理,从销售部门随机抽取了2019年度某一销售小组的月均销售额,该小组各组员2019年度的月均销售额(单位:万元)分别为:3.35,3.35,3.38,3.41,3.43,3.44,3.46,3.48,3.51,3.54,3.56,3.56,3.57,3.59,3.60,3.64,3.64,3.67,3.70,3.70.
(Ⅰ)根据公司人力资源部门的要求,若月均销售额超过3.52万元的组员不低于全组人数的![]() ,则对该销售小组给予奖励,否则不予奖励.试判断该公司是否需要对抽取的销售小组发放奖励;
,则对该销售小组给予奖励,否则不予奖励.试判断该公司是否需要对抽取的销售小组发放奖励;
(Ⅱ)在该销售小组中,已知月均销售额最高的5名销售员中有1名的月均销售额造假.为找出月均销售额造假的组员,现决定请专业机构对这5名销售员的月均销售额逐一进行审核,直到能确定出造假组员为止.设审核次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质量是企业的生命线,某企业在一个批次产品中随机抽检![]() 件,并按质量指标值进行统计分析,得到表格如表:
件,并按质量指标值进行统计分析,得到表格如表:
质量指标值 | 等级 | 频数 | 频率 |
| 三等品 | 10 | 0.1 |
| 二等品 | 30 |
|
| 一等品 |
| 0.4 |
| 特等品 | 20 | 0.2 |
合计 |
| 1 | |
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)从质量指标值在![]() 的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.
的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当a=-2时,求函数f(x)的极值;
(2)若ln[e(x+1)]≥2- f(-x)对任意的x∈[0,+∞)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学对函数![]() 进行研究后,得出以下结论,其中正确的有( )
进行研究后,得出以下结论,其中正确的有( )
A.函数![]() 的图象关于原点对称
的图象关于原点对称
B.对定义域中的任意实数![]() 的值,恒有
的值,恒有![]() 成立
成立
C.函数![]() 的图象与
的图象与![]() 轴有无穷多个交点,且每相邻两交点间距离相等
轴有无穷多个交点,且每相邻两交点间距离相等
D.对任意常数![]() ,存在常数
,存在常数![]() ,使函数
,使函数![]() 在
在![]() 上单调递减,且
上单调递减,且![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com