
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠DAB=60°,AD⊥PD,点F为棱PD的中点.
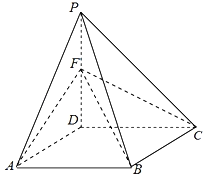
(1)在棱BC上是否存在一点E,使得CF∥平面PAE,并说明理由;
(2)若AC⊥PB,二面角D﹣FC﹣B的余弦值为![]() 时,求直线AF与平面BCF所成的角的正弦值.
时,求直线AF与平面BCF所成的角的正弦值.
【答案】(1)存在,见解析(2)![]() .
.
【解析】
(1)取点E为棱BC的中点,取PA的中点Q,连结EQ、FQ,利用已知结合三角形中位线定理可证四边形CEQF为平行四边形,得到CF∥EQ,再由直线与平面平行的判定得CF∥平面PAE;
(2)取AB中点M,以D为坐标原点,分别以DM,DC,DP所在直线为x,y,z轴建立空间直角坐标系.设FD=a,利用平面FBC与平面DFC的所成角的余弦值求得a,可得平面BCF的一个法向量及![]() 的坐标再由两向量所成角的余弦值可得FA与平面BCF所成的角的正弦值.
的坐标再由两向量所成角的余弦值可得FA与平面BCF所成的角的正弦值.
(1)在棱BC上存在点E,使得CF∥平面PAE,点E为棱BC的中点.
证明:取PA的中点Q,连结EQ、FQ,
由题意,FQ∥AD且![]() ,CE∥AD且
,CE∥AD且![]() ,
,
故CE∥FQ且CE=FQ.
∴四边形CEQF为平行四边形.
∴CF∥EQ,又![]() 平面PAE,
平面PAE,![]() 在平面PAE内,
在平面PAE内,
∴CF∥平面PAE;
(2)取AB中点M,
以D为坐标原点,分别以DM,DC,DP所在直线为x,y,z轴建立空间直角坐标系.
设FD=a,则D(0,0,0),F(0,0,a),C(0,2,0),
B(![]() ,1,0),A(
,1,0),A(![]() ).
).
![]() ,
,![]() .
.
设平面FBC的一个法向量为![]() .
.
由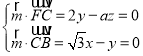 ,取x=1,得
,取x=1,得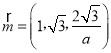 ;
;
取平面DFC的一个法向量为![]() .
.
由题意,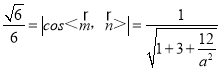 ,解得a
,解得a![]() .
.
∴![]() .
.
设直线AF与平面BCF所成的角为θ,
则![]()
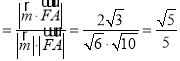 .
.
即直线AF与平面BCF所成的角的正弦值为![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】假设你有一笔资金,现有三种投资方案,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
现打算投资10天,三种投资方案的总收益分别为![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点S( -2,0) ,T(2,0),动点P为平面上一个动点,且直线SP、TP的斜率之积为![]() .
.
(1)求动点P的轨迹E的方程;
(2)设点B为轨迹E与y轴正半轴的交点,是否存在直线l,使得l交轨迹E于M,N两点,且F(1,0)恰是△BMN的垂心?若存在,求l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图,下列描述正确的是( ).
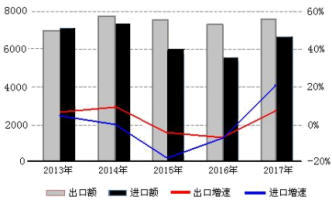
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,其右焦点F到其右准线的距离为1,离心率为
,其右焦点F到其右准线的距离为1,离心率为![]() ,A,B分别为椭圆
,A,B分别为椭圆![]() 的上、下顶点,过点F且不与x轴重合的直线l与椭圆
的上、下顶点,过点F且不与x轴重合的直线l与椭圆![]() 交于C,D两点,与y轴交于点P,直线
交于C,D两点,与y轴交于点P,直线![]() 与
与![]() 交于点Q.
交于点Q.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com