
 ,
, ,
,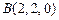 ,∴
,∴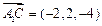 ,
,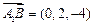 (6分)
(6分)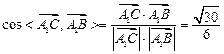 (7分)
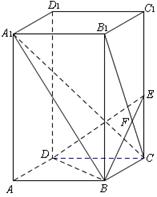
(7分) 平面BDE=K,
平面BDE=K,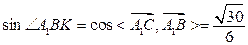 (9分)
(9分)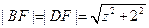 ,
,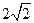 ,故△DBF是等腰三角形,要证明它为锐角三角形,只需证明其顶角∠DFB为锐角则可。 (11分)
,故△DBF是等腰三角形,要证明它为锐角三角形,只需证明其顶角∠DFB为锐角则可。 (11分)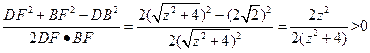


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源:不详 题型:解答题
 平面
平面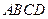 ,
,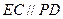 ,且
,且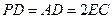 ="2" .
="2" .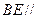 平面
平面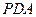 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
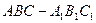 中,
中,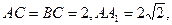 ∠ACB=90°,M是
∠ACB=90°,M是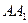 的中点,N是
的中点,N是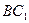 的中点。
的中点。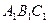 ;
;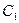 到平面BMC的距离;
到平面BMC的距离;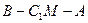 1的大小。
1的大小。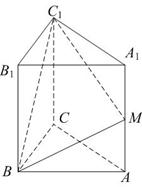
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
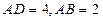 ,E、F分别是线段AB、BC的中点,
,E、F分别是线段AB、BC的中点,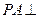 面ABCD. (1)
面ABCD. (1)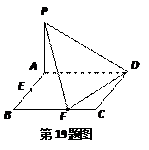 证明:PF⊥FD;
证明:PF⊥FD;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
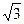 ,BC=CD=3,AC=
,BC=CD=3,AC=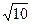 ,BD=2.
,BD=2.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
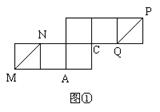
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com