练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知定点，横坐标不小于的动点在轴上的射影为，若.

    （1）求动点的轨迹的方程；

    （2）若点不在直线上，并且直线与曲线相交于两个不同点.问是否存在常数使得当的值变化时，直线斜率之和是一个定值.若存在，求出的值；若不存在，请说明理由.

    【答案】（1）（2）见解析

    【解析】

    (1)利用抛物线定义，即可得到动点的轨迹的方程；

    (2) 设，则，利用韦达定理即可得到结果.

    （1）设点在直线上的射影是，则由于的横坐标不小于，

    所以，又所以

    即点到的距离与到直线的距离相等，所以的轨迹是以为焦点，以为准线的抛物线.

    即的方程是

    （2）由于在曲线上，可设，则

    的斜率的斜率

    所以

    又曲线与直线相交于两点，所以，于是联立方程，得

    ，所以.

    ∴=1-，

    此式随着m的变化，值也在变化，所以不存在k值满足题意.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在圆锥中，，是上的动点，是的直径，，是的两个三等分点，，记二面角，的平面角分别为，，若，则的最大值是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆O；x2+y2=4，F1（-1，0），F2（1，0），点D圆O上一动点，2=，点C在直线EF1上，且=0，记点C的轨迹为曲线W．

    （1）求曲线W的方程；

    （2）已知N（4，0），过点N作直线l与曲线W交于A，B不同两点，线段AB的中垂线为l'，线段AB的中点为Q点，记P与y轴的交点为M，求|MQ|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动圆过定点，且和直线相切，动圆圆心形成的轨迹是曲线，过点的直线与曲线交于两个不同的点.

    （1）求曲线的方程；

    （2）在曲线上是否存在定点，使得以为直径的圆恒过点？若存在，求出点坐标；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某小区为了调查居民的生活水平，随机从小区住户中抽取个家庭，得到数据如下：

    家庭编号

    1

    2

    3

    4

    5

    6

    月收入x（千元）

    20

    30

    35

    40

    48

    55

    月支出y（千元）

    4

    5

    6

    8

    8

    11

    参考公式：回归直线的方程是：，其中， .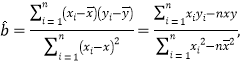

    （1）据题中数据，求月支出（千元）关于月收入（千元）的线性回归方程（保留一位小数）；

    （2）从这个家庭中随机抽取个，求月支出都少于万元的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体中，四边形为直角梯形，，，四边形为矩形，平面平面，，，点为的中点，点为的中点.

    （1）求证：；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为响应党中央号召，学校以“我们都是追梦人”为主题举行知识竞赛。现有10道题，其中6道甲类题，4道乙类题，王同学从中任取3道题解答.

    （Ⅰ）求王同学至少取到2道乙类题的概率;

    （Ⅱ）如果王同学答对每道甲类题的概率都是，答对每道乙类题的概率都是，且各题答对与否相互独立，已知王同学恰好选中2道甲类题，1道乙类题，用表示王同学答对题的个数，求随机变量的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图（1），在直角梯形中，为的中点，四边形为正方形，将沿折起，使点到达点，如图（2），为的中点，且，点为线段上的一点.

    （1）证明：；

    （2）当与夹角最小时，求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，其中．

    （Ⅰ）当为偶函数时，求函数的极值；

    （Ⅱ）若函数在区间上有两个零点，求的取值范围．

    查看答案和解析>>

    同步练习册答案