解:(Ⅰ)当a=2时,f(x)=xe
-x+(x-2)e
x-2,f(x)的定义域为R,
f′(x)=e
-x-xe
-x+e
x-2+(x-2)e
x-2=(x-1)(e
x-2-e
-x)=e
-x(x-1)(e
x-1-1)(e
x-1+1).
当x≥1时,x-1≥0,e
x-1-1≥0,所以f′(x)≥0,
当x<1时,x-1<0,e
x-1-1<0,所以f′(x)≥0,
所以对任意实数x,f′(x)≥0,
所以f(x)在R上是增函数;
(II)当x≥1时,f(x)≥
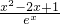
恒成立,即(x-2)e
2x-a-x
2+3x-1≥0恒成立,
设h(x)=(x-2)e
2x-a-x
2+3x-1(x≥1),则h′(x)=(2x-3)(e
2x-a-1),
令h′(x)=(2x-3)(e
2x-a-1)=0,解得

,
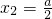
,
(1)当1<

<

,即2<a<3时,
| x | (1, ) ) |  | ( , , ) ) |  | ( ,+∞) ,+∞) |
| h′(x) | + | 0 | - | 0 | + |
| h(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
所以要使结论成立,则h(1)=-e
2-a+1≥0,h(

)=-

e
3-a+

≥0,即e
2-a≤1,e
3-a≤

,
解得a≥2,a≥3-ln

,所以3-ln

≤a<3;
(2)当

=

,即a=3时,h′(x)≥0恒成立,所以h(x)是增函数,又h(1)=-e
-1+1>0,
故结论成立;
(3)当
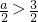
,即a>3时,
| x | (1, ) ) |  | ( , , ) ) |  | ( ,+∞) ,+∞) |
| h′(x) | + | 0 | - | 0 | + |
| h(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
所以要使结论成立,
则h(1)=-e
2-a+1≥0,h(

)=-

+2a-3≥0,即e
2-a≤1,a
2-8a+12≤0,
解得a≥2,2≤a≤6,所以3<a≤6;
综上所述,若a>2,当x≥1时,f(x)≥
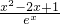
恒成立,实数a的取值范围是3-ln

≤a≤6. …(12分)
分析:(Ⅰ)只需证明当a=2时f′(x)≥0恒成立即可;
(Ⅱ)当x≥1时,f(x)≥
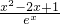
恒成立,即(x-2)e
2x-a-x
2+3x-1≥0恒成立,设h(x)=(x-2)e
2x-a-x
2+3x-1(x≥1),从而转化为h(x)
min≥0即可,利用导数可求得h(x)
min,注意对a进行讨论;
点评:本题考查利用导数研究函数单调性、求函数最值问题,考查不等式恒成立问题,考查学生分类讨论思想.

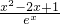 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.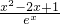 恒成立,即(x-2)e2x-a-x2+3x-1≥0恒成立,
恒成立,即(x-2)e2x-a-x2+3x-1≥0恒成立, ,
,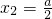 ,
, <
< ,即2<a<3时,
,即2<a<3时, )
)
 ,
, )
)
 ,+∞)
,+∞) )=-
)=- e3-a+
e3-a+ ≥0,即e2-a≤1,e3-a≤
≥0,即e2-a≤1,e3-a≤ ,
, ,所以3-ln
,所以3-ln ≤a<3;
≤a<3; =
= ,即a=3时,h′(x)≥0恒成立,所以h(x)是增函数,又h(1)=-e-1+1>0,
,即a=3时,h′(x)≥0恒成立,所以h(x)是增函数,又h(1)=-e-1+1>0,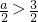 ,即a>3时,
,即a>3时, )
)
 ,
, )
)
 ,+∞)
,+∞) )=-
)=- +2a-3≥0,即e2-a≤1,a2-8a+12≤0,
+2a-3≥0,即e2-a≤1,a2-8a+12≤0,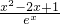 恒成立,实数a的取值范围是3-ln
恒成立,实数a的取值范围是3-ln ≤a≤6. …(12分)
≤a≤6. …(12分)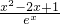 恒成立,即(x-2)e2x-a-x2+3x-1≥0恒成立,设h(x)=(x-2)e2x-a-x2+3x-1(x≥1),从而转化为h(x)min≥0即可,利用导数可求得h(x)min,注意对a进行讨论;
恒成立,即(x-2)e2x-a-x2+3x-1≥0恒成立,设h(x)=(x-2)e2x-a-x2+3x-1(x≥1),从而转化为h(x)min≥0即可,利用导数可求得h(x)min,注意对a进行讨论;

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<