练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】当时，不等式成立，则实数k的取值范围是______________.

    【答案】k∈（﹣∞，1]

    【解析】

    此题先把常数k分离出来，再构造成再利用导数求函数的最小值，使其最小值大于等于k即可．

    由题意知：

    ∵当0≤x≤1时

    （1）当x＝0时，不等式恒成立 k∈R

    （2）当0＜x≤1时，不等式可化为

    要使不等式恒成立，则k成立

    令f（x） x∈（0，1]

    即 f '（x）

    再令g（x）

    g'（x）

    ∵当0＜x≤1时，g'（x）＜0

    ∴g（x）为单调递减函数

    ∴g（x）＜g（0）＝0

    ∴f '（x）＜0

    即函数f（x）为单调递减函数

    所以 f（x）min＝f（1）＝1 即k≤1

    综上所述，由（1）（2）得 k≤1

    故答案为： k∈（﹣∞，1]．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】

    已知函数在区间，内各有一个极值点．

    （I）求的最大值；

    （II）当时，设函数在点处的切线为，若在点处穿过函数的图象（即动点在点附近沿曲线运动，经过点时，从的一侧进入另一侧），求函数的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24，16，16.现采用分层抽样的方法从中抽取7人，进行睡眠时间的调查.

    （I）应从甲、乙、丙三个部门的员工中分别抽取多少人？

    （II）若抽出的7人中有4人睡眠不足，3人睡眠充足，现从这7人中随机抽取3人做进一步的身体检查.

    （i）用X表示抽取的3人中睡眠不足的员工人数，求随机变量X的分布列与数学期望；

    （ii）设A为事件“抽取的3人中，既有睡眠充足的员工，也有睡眠不足的员工”，求事件A发生的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在极坐标系中，，，，，，弧，所在圆的圆心分别是，，曲线是弧，曲线是线段，曲线是线段，曲线是弧.

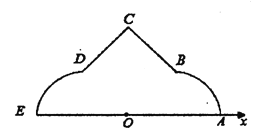
    （1）分别写出，，，的极坐标方程；

    （2）曲线由，，，构成，若点，（），在上，则当时，求点的极坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了研究某种细菌的繁殖个数y随天数x的变化情况，收集数据如下：

    天数x

    1

    2

    3

    4

    5

    6

    繁殖个数y

    6

    12

    25

    49

    95

    190

    （1）根据散点图，判断与哪一个适合作为y关于x的回归方程类型；（给出判断即可，不用说明理由）

    （2）根据（1）中的判断及表中数据，求y关于x的回归方程参考数据：，，，，，

    参考公式：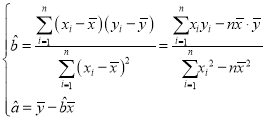

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】新冠状病毒严重威胁着人们的身体健康，我国某医疗机构为了调查新冠状病毒对我国公民的感染程度，选了某小区的位居民调查结果统计如下：

    感染

    不感染

    合计

    年龄不大于岁

    年龄大于岁

    合计

    （1）根据已知数据，把表格数据填写完整；

    （2）能否在犯错误的概率不超过的前提下认为感染新冠状病与不同年龄有关？

    （3）已知在被调查的年龄大于岁的感染者中有名女性，其中位是女教师，现从这名女性中随机抽取人，求至多有位教师的概率．

    附：，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆周上有七个不同的点，以其中任意一点为始点，另一点为终点作向量，作出所有的向量（对于点、，若作出向量，则不再作向量）.若其中某四点所确定的凸四边形的四条边是首尾相接的四个向量，则称其为“零四边形”.试求以这七个点中四个点为顶点的凸四边形中，零四边形个数的最大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了研究“教学方式”对教学质量的影响，某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学（勤奋程度和自觉性都一样）.以下茎叶图为甲、乙两班（每班均为20人）学生的数学期末考试成绩．

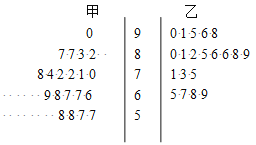
    （1）学校规定：成绩不低于75分的为优秀．请画出下面的列联表．

    甲班

    乙班

    合计

    优秀

    不优秀

    合计

    （2）判断有多大把握认为“成绩优秀与教学方式有关”．

    下面临界值表仅供参考：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    参考公式：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，左顶点为，过椭圆的右焦点作互相垂直的两条直线分别交直线于两点，交椭圆于另一点.

    （Ⅰ）求椭圆的方程；

    （Ⅱ）求证：直线恒过定点，并求出定点坐标．

    查看答案和解析>>

    同步练习册答案