
分析 分析知如两船到达的时间间隔超过了停泊的时间则不需要等待,要求一艘船停靠泊位时必须等待一段时间的概率;即计算一船到达的时间恰好另一船还没有离开,此即是所研究的事件.
解答  解:设甲船在x点到达,乙船在y点到达,必须等待的事件需要满足如下条件:
解:设甲船在x点到达,乙船在y点到达,必须等待的事件需要满足如下条件:
$\left\{\begin{array}{l}{0≤x≤24}\\{0≤y≤24}\\{y-x≤2}\\{x-y≤4}\end{array}\right.$,
画出不等式组表示的平面区域如图所示;
所以p(A)=1-$\frac{\frac{1}{2}×20×20+\frac{1}{2}×22×22}{24×24}$=$\frac{67}{288}$;
所以一艘船停靠泊位时必须等待一段时间的概率是$\frac{67}{288}$.
故答案为:$\frac{67}{288}$.
点评 本题考查了几何概型的应用问题,解题的关键是得出所给的事件对应的约束条件及作出符合条件的图象,由图形的测度得出相应的概率.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
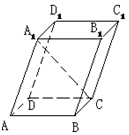 如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为1的正方形,若∠A1AB=∠A1AD=60°,且A1C=$\sqrt{5}$,则A1A=3.
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为1的正方形,若∠A1AB=∠A1AD=60°,且A1C=$\sqrt{5}$,则A1A=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{20}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=|x| | B. | y=1-x | C. | y=$\frac{1}{x}$ | D. | y=-x2+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y=0 | B. | x+y+3=0 | C. | x-y+3=0 | D. | x+y+3=0或2x+y=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com