
分析 由题意得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出甲投中蓝的次数X的数学期望.
解答 解:由题意得X的可能取值为0,1,2,3,
P(X=0)=(1-$\frac{2}{3}$)4=$\frac{1}{81}$,
P(X=1)=${C}_{4}^{1}(\frac{2}{3})(1-\frac{2}{3})^{3}$=$\frac{8}{81}$,
P(X=2)=${C}_{4}^{2}(\frac{2}{3})^{2}(1-\frac{2}{3})^{2}$=$\frac{24}{81}$,
P(X=3)=1-($\frac{1}{81}+\frac{8}{81}+\frac{24}{81}$)=$\frac{48}{81}$,
∴EX=0×$\frac{1}{81}+1×\frac{8}{81}+2×\frac{24}{81}+3×\frac{48}{81}$=$\frac{200}{81}$.
故答案为:$\frac{200}{81}$.
点评 本题考查离散型随机变量的数学期望的求法,是基础题,解题时要注意n次独立重复试验中事件A恰好发生k的概率公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 59 | B. | 60 | C. | 61 | D. | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
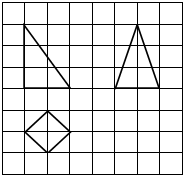 如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )| A. | $\sqrt{2}$+$\sqrt{6}$ | B. | 2+2$\sqrt{6}$ | C. | 2+2$\sqrt{2}$+2$\sqrt{6}$ | D. | 2+3$\sqrt{2}$+$\sqrt{22}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com