Question

若函数y＝f(x)在x＝x0处取得极大值或极小值，则称x0为函数y＝f(x)的极值点．已知A，b是实数，1和－1是函数f(x)＝x3＋Ax2＋b x的两个极值点．

(1)求A和b的值；

(2)设函数g(x)的导函数g′(x)＝f(x)＋2，求g(x)的极值点．

 

Answer 1

(1) ；(2) 函数g(x)的极值点为．

【解析】

试题分析：(1)极值点时，函数取得极值，对应的导函数的值为，先对函数求导得，当取时，导函数值为，得到关于的二元一次方程，解得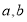的值；(2) 由知，令得或，两数将定义域分成三个部分，根据极值定义列表判断，可知当时函数有极小值．

【解析】
(1)因为，

所以f′(x)＝3x2＋2Ax＋b，且f′(－1)＝3－2A＋b＝0，f′(1)＝3＋2A＋b＝0，

解得A＝0，b＝－3． 4分

经检验，当A＝0，b＝－3时，1和－1是函数f(x)＝x3＋Ax2＋bx的两个极值点．

综上，所求的A和b的值分别为0，－3． 5分

(2)由(1)，知f(x)＝x3－3x，所以g′(x)＝x3－3x＋2＝(x－1)2(x＋2)，

令g′(x)＝0，得x＝1或x＝－2， 7分

当x变化时，g′(x)，g(x)的变化情况如下所示：

x	(－∞，－2)	－2	(－2,1)	1	(1，＋∞)
g′(x)	－	0	＋	0	＋
g(x)	↘?	极小值	↗?	不是极值	↗

11分

所以x＝－2是函数g(x)的极小值点，

即函数g(x)的极值点为－2． 12分

考点：利用导数求函数的极值．