
分析 (Ⅰ)由${S_n}=2{a_n}-{a_1},n∈{N^*}$,利用当n≥2时,an=Sn-Sn-1,整理得an=2an-1,利用等比数列的定义及其通项公式即可得出.
(Ⅱ)由(Ⅰ)知,{an}是公比为2的等比数列.对5am为ap,aq三项的顺序分类讨论,利用等差数列的通项公式及其性质即可得出.
(III)由${a_n}={a_1}•{2^{n-1}}$,得$|{t_n}|=|{r_n}|={a_1}•{2^{n-1}}$,可得:t100=r100或t100=-r100,若t100=-r100,不妨设t100>0,r100<0,则${T_{100}}={t_1}+{t_2}+…+{t_{99}}+{t_{100}}≥-{a_1}-{a_1}•2-{a_1}•{2^2}-…-{a_1}•{2^{98}}+{a_1}•{2^{99}}$=a1.则${R_{100}}={r_1}+{r_2}+…+{r_{99}}+{r_{100}}≤{a_1}+{a_1}•2+{a_1}•{2^2}+…+{a_1}•{2^{98}}-{a_1}•{2^{99}}$=-a1.
由已知a1>0,∴R100<T100,与已知不符,因此t100=r100,同理可得R99=T99,如此下去,t98=r98,…,t1=r1,.
解答 解:(Ⅰ)∵${S_n}=2{a_n}-{a_1},n∈{N^*}$,∴Sn-1=2an-1-a1,
∴当n≥2时,an=Sn-Sn-1=(2an-a1)-(2an-1-a1),整理得an=2an-1,
又an>0,∴$\frac{a_n}{{{a_{n-1}}}}$=2,数列{an}是公比为2的等比数列,
∴数列{an}的通项公式${a_n}={2^{n-1}}$.
(Ⅱ)由(Ⅰ)知,{an}是公比为2的等比数列.
①若5am为ap,aq的等差中项,则2×5am=ap+aq,
∴$2×5{a_1}{2^{m-1}}={a_1}{2^{p-1}}+{a_1}{2^{q-1}}$,化为2p-m-1+2q-m-1=5,
又m<p<q,m,p,q∈N*,∴2p-m-1=1,2q-m-1=4,
∴p-m-1=0,q-m-1=2.即p=m+1,q=m+3.
②若ap为5am,aq的等差中项,则2ap=5am+aq,
∴$2{a_1}{2^{p-1}}=5{a_1}{2^{m-1}}+{a_1}{2^{p-1}}$,∴2p=5×2m-1+2q-1,
∴2p-m+1-2q-m=5,等式左边为偶数,右边为奇数,等式不成立,舍去.
③若aq为5am,ap的等差中项,则2aq=5am+ap,同理也不成立.
综上,p=m+1,q=m+3.
(Ⅲ)由${a_n}={a_1}•{2^{n-1}}$,得$|{t_n}|=|{r_n}|={a_1}•{2^{n-1}}$,
∴t100=r100或t100=-r100,
若t100=-r100,不妨设t100>0,r100<0,
则${T_{100}}={t_1}+{t_2}+…+{t_{99}}+{t_{100}}≥-{a_1}-{a_1}•2-{a_1}•{2^2}-…-{a_1}•{2^{98}}+{a_1}•{2^{99}}$=$-{a_1}(1+2+{2^2}+…+{2^{98}})+{a_1}•{2^{99}}=-{a_1}×\frac{{1-{2^{99}}}}{1-2}+{a_1}•{2^{99}}={a_1}$.
则${R_{100}}={r_1}+{r_2}+…+{r_{99}}+{r_{100}}≤{a_1}+{a_1}•2+{a_1}•{2^2}+…+{a_1}•{2^{98}}-{a_1}•{2^{99}}$=${a_1}(1+2+{2^2}+…+{2^{98}})-{a_1}•{2^{99}}={a_1}×\frac{{1-{2^{99}}}}{1-2}-{a_1}•{2^{99}}=-{a_1}$.
由已知a1>0,∴R100<T100,与已知不符,∴t100=r100,
∴R99=T99,同上可得t99=r99,
如此下去,t98=r98,…,t1=r1,
即对于任意的正整数k(1≤k≤100),均有tk=rk成立.
点评 本题考查了等差数列与等比数列的通项公式及其求和公式、分类讨论方法,考查了推理能力与计算能力,属于难题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(?q) | C. | (?p)∧q | D. | (?p)∧(?q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{16}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期为π | |
| B. | 直线x=$\frac{π}{12}$是函数f(x)图象的对称轴 | |
| C. | 函数f(x)的图象关于点(-$\frac{π}{6}$,0)对称 | |
| D. | 函数f(x)在区间(-$\frac{π}{12}$,$\frac{5π}{12}$)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 成绩等级 | A | B | C | D | E |
| 成绩(分) | 100 | 85 | 70 | 60 | 50以下 |
| 人数(名) | 1 | a | b | 8 | c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
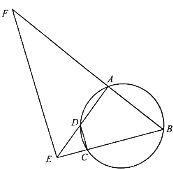 如图,圆内接四边形ABCD的边BC与AD的延长线交于点E,点F在BA的延长线上.
如图,圆内接四边形ABCD的边BC与AD的延长线交于点E,点F在BA的延长线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com