
���� ��1��������ɵ�f��2��=5.2�����a=-4������2��x��15ʱ����õ����͵������䡢��ֵ����ֵ����0��x��2ʱ��f��x���ĵ����Կɵ�f��x�������ֵ��
��2������0��x��2ʱ��f��x����0��x�ķ�Χ����f��x����[2��15]�Ķ˵�ĺ���ֵ���ɵ�f��x����0�������ж���ҵ������x�ķ�Χ��
��� �⣺��1���������֪����x=2ʱ��f��2��=5.2��
����aln2-$\frac{1}{4}$��22+$\frac{9}{2}$��2=5.2�����a=-4��
��f��x��=$\left\{\begin{array}{l}{2{x}^{2}-��2ln2��x��0��x��2}\\{-4lnx-\frac{1}{4}{x}^{2}+\frac{9}{2}x��2��x��15}\end{array}\right.$��
��2��x��15ʱ��f��x��=-4lnx-$\frac{1}{4}$x2+$\frac{9}{2}$x��
f�䣨x��=-$\frac{4}{x}$-$\frac{1}{2}$x+$\frac{9}{2}$=-$\frac{��x-1����x-8��}{2x}$��
��2��x��8ʱ��f�䣨x����0��f��x��������
��8��x��15ʱ��f�䣨x����0��f��x���ݼ���
��2��x��15ʱ��f��x��max=f��8��=-4ln8-16+36=11.6��
��0��x��2ʱ��f��x����2��4-��2ln2����2=5.2��
�ʸ�С��ҵͶ��8��Ԫʱ����õľ��������
��2����0��x��2ʱ��2x2-��2ln2��x��0��
���0��x��ln2������ҵ������
��2��x��15ʱ��f��2��=5.2��f��15��=-4ln15-$\frac{1}{4}$��152+$\frac{9}{2}$��15=0.45��0��
��f��x��min=f��15��=0.45��0��
���Ͽɵã�0��x��ln2����0��x��0.7ʱ������ҵ������
���� ���⿼�鵼����ʵ�������е����ã�����ֵ�����黯��������������������ȷ���ǽ���Ĺؼ��������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǰ�ԲO��ֱ����P��AB���ӳ����ϣ�PD���ԲO�����ڵ�C��AD��PD����PC=2��PB=1����CD=1.2��
��ͼ��AB�ǰ�ԲO��ֱ����P��AB���ӳ����ϣ�PD���ԲO�����ڵ�C��AD��PD����PC=2��PB=1����CD=1.2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
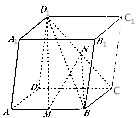 ��ͼ�����ⳤΪ2��������ABCD-A1B1C1D1�У�AB��D1C���е�ֱ���M��N
��ͼ�����ⳤΪ2��������ABCD-A1B1C1D1�У�AB��D1C���е�ֱ���M��N�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | D⊆A | B�� | D=B | C�� | D⊆C | D�� | D=C |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
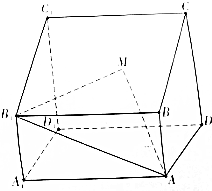 ��ͼ��ֱ������ABCD-A1B1C1D1�У�����ABCD��ֱ�����Σ�AB��CD��AD��CD��2AB=CD������AA1D1D�Ͳ���CC1D1D�������Σ�M�Dz���CC1D1D�����ģ�
��ͼ��ֱ������ABCD-A1B1C1D1�У�����ABCD��ֱ�����Σ�AB��CD��AD��CD��2AB=CD������AA1D1D�Ͳ���CC1D1D�������Σ�M�Dz���CC1D1D�����ģ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
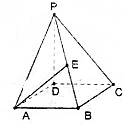 ����P-ABCD�У������DZ߳�Ϊ6�����Σ��ҡ�BAD=60�㣬PD��ƽ��ABCD��PD=8��
����P-ABCD�У������DZ߳�Ϊ6�����Σ��ҡ�BAD=60�㣬PD��ƽ��ABCD��PD=8���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com