Question

（08年天津南开区质检理） （12分）

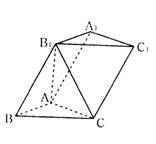
如图，已知三棱柱的各棱长均为2，侧棱与底面ABC所成的角为，且侧面垂直于底面ABC。

（1）证明；

（2）求三棱锥的体积；

（3）求二面角的大小。（用反三角函数表示）

 

Answer 1

解析：本小题考查直线与直线垂直、直线与平面垂直、平面与平面垂直、二面角的概念、棱锥体积公式等基础知识，考查空间想象能力、运算能力和推理论证能力。

    （1）证明：在平面ABB₁A₁内，过B₁作B_­1D⊥AB于D

∵ 侧面ABB₁A₁⊥平面ABC    ∴ B₁D⊥平面ABC

∴ ∠B₁BA是B₁B与底面ABC所成角，∠B₁BA=

∵ 三棱柱各棱长均为2，△B₁BA为正三角形

∴ D是AB中点，连CD，在正△ABC中，CD⊥AB

∴ AB⊥CB₁（4分）

（2）解：∵ B₁D⊥平面ABC    ∴ B₁D是三棱锥的高

由，得

∴ （8分）

（3）解：∵ △ABC为正三角形，CD⊥AB，CD⊥B₁D，AB∩B₁D=D

∴ CD⊥平面ABB₁

在平面ABB₁中作DE⊥AB₁于E，连结CE，则CE⊥AB₁

∴ ∠CED为二面角的平面角（10分）

在中，

连结BA₁交AB₁于O，则BO=

∴    ∴

∴ 所求二面角的大小为（12分）