分析:(1)由题意可得 f(0)=0,且 f(-1)=-f(1),由此求得a和b的值,即可求得a+b的值.
(2)由题意可得
f() = f(x-k) 有两个解,即函数y=
与函数 y=x-k有两个交点,数形结合求得k的取值范围.
解答:解:(1)∵定义域为R的函数
f(x)= 时奇函数,
∴f(0)=0,且 f(-1)=-f(1),
即 b=2°=1,
=-
,解得 a=2,b=1,故a+b=3.
故答案为 3.
(2)函数
g(x)=f()+f(k-x)有两个零点,即
f() = -f(k-x) 有两个解.
再由f(x)是奇函数,可得
f() = f(x-k) 有两个解,
故方程
=(x-k)有两个解,即函数y=
与函数 y=x-k有两个交点.
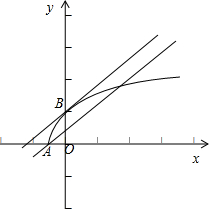
如图所示:当直线 y=x-k过点A(-
,0)时,y=
的图象与 y=x-k的图象有两个交点,此时k=-
.
当y=
与 y=x-k相切时,对于函数y=
,令其导数为y′=
=1,可得 x=0,此时,y=x-k与y=
相切于点B(0,1),
把点B(0,1)代入 y=x-k可得 k=-1.
结合图象可得,当-1<k≤-
时,函数y=
的图象与函数 y=x-k的图象有两个交点,
故k的取值范围是(-1,-
].
故答案为 (-1,-
].
点评:本题主要考查了奇函数的性质,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于基础题.




 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案