练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若关于x的方程 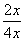= kx + 1-2k(k为实数)有三个实数解，则这三个实数解的和 _ .


    6 . 提示：两个函数的图象均关于点（2，0）对称.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn，且满足Sn＋n＝2an(n∈N*)．

    (1)证明：数列{an＋1}为等比数列，并求数列{an}的通项公式；

    (2)若bn＝(2n＋1)an＋2n＋1，数列{bn}的前n项和为Tn.求满足不等式>2 010的n的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列为等比数列，前项和为，若，，且、、

    成等差数列，则数列的通项公式         ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设数列{an}，{bn}满足a1=b1，且对任意正整数n，{an}中小于等于n的项数恰为bn；{bn}中小于等于n的项数恰为an．

        （1）求a1；

        （2）求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     若以连续掷两次骰子分别得到的点数m、n作为点P的横、纵坐标，则点P在直线x＋y = 5下方的概率为          ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，有一块矩形草坪ABCD，AB=100米，BC=米，欲在这块草坪内铺设三条小路OE、EF和OF，要求O是AB的中点，点E在边BC上，点F在边AD上，且∠EOF=90°；

    （1）设∠BOE=，试求的周长关于的函数解析式，并求出此函数的定义域；

    （2）经核算，三条路每米铺设费用均为400元，试问如何设计才能使铺路的总费用最低？

    并求出最低总费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设x，y均为正数，且x＞y，求证：2x＋≥2y＋3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    过的光线经轴上点反射后，经过不等式组所表示的区域，则的取值范围        ；

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    当x<时，求函数y＝x＋的最大值．

    查看答案和解析>>

    同步练习册答案