
已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式 >2 010的n的最小值.
>2 010的n的最小值.
(1)因为Sn+n=2an,所以Sn-1=2an-1-(n-1)(n≥2,n∈N*).两式相减,得an=2an-1+1.
所以an+1=2(an-1+1)(n≥2,n∈N*),所以数列{an+1}为等比数列.
因为Sn+n=2an,令n=1得a1=1.
a1+1=2,所以an+1=2n,所以an=2n-1.
(2)因为bn=(2n+1)an+2n+1,所以bn=(2n+1)·2n.
所以Tn=3×2+5×22+7×23+…+(2n-1)·2n-1+(2n+1)·2n, ①
2Tn=3×22+5×23+…+(2n-1)·2n+(2n+1)·2n+1, ②
①-②,得-Tn=3×2+2(22+23+…+2n)-(2n+1)·2n+1
=6+2×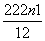 -(2n+1)·2n+1
-(2n+1)·2n+1
=-2+2n+2-(2n+1)·2n+1=-2-(2n-1)·2n+1.
所以Tn=2+(2n-1)·2n+1.
若 >2 010,
>2 010,
则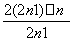 >2 010,即2n+1>2 010.
>2 010,即2n+1>2 010.
由于210=1 024,211=2 048,所以n+1≥11,即n≥10.
所以满足不等式 >2 010的n的最小值是10.
>2 010的n的最小值是10.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
汽车从刹车开始到完全静止所用的时间叫做刹车时间;所经过的距离叫做刹车距离.某型汽车的刹车距离s(单位米)与时间t(单位秒)的关系为 ,其中k是一个与汽车的速度以及路面状况等情况有关的量.
,其中k是一个与汽车的速度以及路面状况等情况有关的量.
(1)当k=8时,且刹车时间少于1秒,求汽车刹车距离;
(2)要使汽车的刹车时间不小于1秒钟,且不超过2秒钟,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为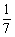 。现有甲、乙两人从袋中轮流、不放回地摸取1球,甲先取,乙后取,然后甲再取……直到袋中的球取完即终止。若摸出白球,则记2分,若摸出黑球,则记1分。每个球在每一次被取出的机会是等可能的。用表示甲,乙最终得分差的绝对值.
。现有甲、乙两人从袋中轮流、不放回地摸取1球,甲先取,乙后取,然后甲再取……直到袋中的球取完即终止。若摸出白球,则记2分,若摸出黑球,则记1分。每个球在每一次被取出的机会是等可能的。用表示甲,乙最终得分差的绝对值.
(1)求袋中原有白球的个数;
(2)求随机变量的概率分布列及期望E.
查看答案和解析>>
科目:高中数学 来源: 题型:
在极坐标系中,圆C的圆心坐标为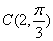 ,半径为2. 以极点为原点,极轴为
,半径为2. 以极点为原点,极轴为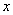 的正半轴,取相同的长度单位建立平面直角坐标系,直线
的正半轴,取相同的长度单位建立平面直角坐标系,直线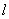 的参数方程为
的参数方程为 (
(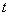 为参数)
为参数)
(1)求圆C的极坐标方程;
(2)设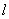 与圆C的交点为
与圆C的交点为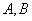 ,
, 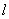 与
与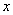 轴的交点为
轴的交点为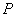 ,求
,求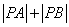
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com