
分析 ①根据三角函数的有界性进行判断.
②根据三角函数的诱导公式进行化简即可.
③根据三角函数的对称性进行判断.
④根据三角函数值的大小关系进行比较即可.
解答 解:①∵sinαcosα=$\frac{1}{2}$sin2α∈[$-\frac{1}{2}$,$\frac{1}{2}$],∵$\frac{\sqrt{3}}{2}$>$\frac{1}{2}$,∴存在实数α,使$sinα•cosα=\frac{{\sqrt{3}}}{2}$错误,故①错误,
②函数$y=sin(\frac{3}{2}π-x)$=cosx是偶函数,故②正确,
③当$x=\frac{π}{8}$时,$y=cos(2x+\frac{3}{4}π)$=cos(2×$\frac{π}{8}$+$\frac{3π}{4}$)=cosπ=-1是函数的最小值,则$x=\frac{π}{8}$是函数$y=cos(2x+\frac{3}{4}π)$的一条对称轴方程,故③正确,
④当α=$\frac{π}{4}$,β=$\frac{9π}{4}$,满足α、β是第一象限的角,且α<β,但sinα=sinβ,即sinα<sinβ不成立,故④错误,
故答案为:②③.
点评 本题主要考查命题的真假判断,涉及三角函数的图象和性质,考查学生的运算和推理能力.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (-2,-1) | C. | (-∞,-3) | D. | (-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
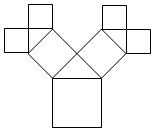 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com