Question

4．班主任为了对本班学生的考试成绩进行分析，决定从全班25名女同学，15名男同学中随机抽取一个容量为8的样本进行分析．
（Ⅰ）如果按性别比例分层抽样，可以得到多少个不同的样本？（只要求写出计算式即可，不必计算出结果）
（Ⅱ）随机抽取8位，他们的数学分数从小到大排序是：60，65，70，75，80，85，90，95，物理分数从小到大排序是：72，77，80，84，88，90，93，95．
（i）若规定85分以上（包括85分）为优秀，求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率；
（ii）若这8位同学的数学、物理分数事实上对应如下表：

学生编号	1	2	3	4	5	6	7	8
数学分数x	60	65	70	75	80	85	90	95
物理分数y	72	77	80	84	88	90	93	95

根据上表数据，用变量y与x的相关系数或散点图说明物理成绩y与数学成绩x之间线性相关关系的强弱．如果具有较强的线性相关关系，求y与x的线性回归方程（系数精确到0.01）；如果不具有线性相关性，请说明理由．
参考公式：相关系数r=$\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sqrt{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}\sum_{i=1}^n{{{（{y_i}-\overline y）}^2}}}}}}$；回归直线的方程是：$\widehaty=bx+a$，其中对应的回归估计值b=$\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，a=$\overline y-b\overline x$，$\widehat{y_i}$是与x_i对应的回归估计值．
参考数据：$\overline x=77.5，\overline y=84.875，{\sum_{i=1}^8{（{x_i}-\overline x）}^2}≈1050，{\sum_{i=1}^8{（{y_i}-\overline y）}^2}$≈457，$\sum_{i=1}^8{（{x_i}-\overline x）}（{y_i}-\overline y）≈688，\sqrt{1050}≈32.4，\sqrt{457}≈21.4，\sqrt{550}$≈23.5．

Answer 1

分析 （I）根据分层抽样原理计算，使用组合数公式得出样本个数；
（II）（i）使用乘法原理计算；
（ii）根据回归方程计算回归系数，得出回归方程．

解答 解：（I）应选女生$25×\frac{8}{40}=5$位，男生$15×\frac{8}{40}=3$位，可以得到不同的样本个数是$C_{25}^5C_{15}^3$．
（II）（i）这8位同学中恰有3位同学的数学和物理分数均为优秀，则需要先从物理的4个优秀分数中选3个与数学优秀分数对应，种数是$C_4^3A_3^3$（或$A_4^3$），然后将剩下的5个数学分数和物理分数任意对应，种数是$A_5^5$，根据乘法原理，满足条件的种数是$C_4^3A_3^3A_5^5$．这8位同学的物理分数和数学分数分别对应的种数共有$A_8^8$种．
故所求的概率$P=\frac{C_4^3A_3^3A_5^5}{A_8^8}=\frac{1}{14}$．
（ii）变量y与x的相关系数$r≈\frac{688}{32.4×21.4}≈0.99$．可以看出，物理与数学成绩高度正相关．也可以数学成绩x为横坐标，物理成绩y为纵坐标做散点图如下：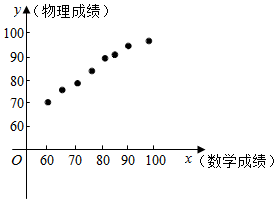

从散点图可以看出这些点大致分布在一条直线附近，并且在逐步上升，故物理与数学成绩高度正相关．
设y与x的线性回归方程是$\widehaty=bx+a$，根据所给数据，可以计算出$b≈\frac{688}{1050}≈0.66$，a=84.875-0.66×77.5≈33.73，
所以y与x的线性回归方程是$\widehaty≈0.66x+33.73$．

点评 本题考查了数据处理，概率计算，回归方程得解法，属于中档题．