
 ��ͼ��ʾ��A��B������������תվ��B��A����������16ǧ�״���AB������Ϊ������������Ϊ�����ƴ�����������������������AB�ı��潨һ���������糧P���������糧P��ѡַ��������������Ҫ��A��B��P�ɿ��������㣩�����������糧������������תվ�ľ���������ÿ�켯�е������������ɷ��ȣ�����ϵ����ͬ�����������糧Ӧ����Զ�������������ο���ָ���ǵ�P��ֱ��AB�ľ���Ҫ�����ܴ��ֹ����A��B������תվÿ�켯�е������������ֱ�ԼΪ30�ֺ�50�֣����������糧�����ѡַ����ͬʱ��������Ҫ��
��ͼ��ʾ��A��B������������תվ��B��A����������16ǧ�״���AB������Ϊ������������Ϊ�����ƴ�����������������������AB�ı��潨һ���������糧P���������糧P��ѡַ��������������Ҫ��A��B��P�ɿ��������㣩�����������糧������������תվ�ľ���������ÿ�켯�е������������ɷ��ȣ�����ϵ����ͬ�����������糧Ӧ����Զ�������������ο���ָ���ǵ�P��ֱ��AB�ľ���Ҫ�����ܴ��ֹ����A��B������תվÿ�켯�е������������ֱ�ԼΪ30�ֺ�50�֣����������糧�����ѡַ����ͬʱ��������Ҫ�� ���� ����������PA=5x��PB=3x���������Ҷ��������ɵõ�cos��PAB����ͬ�ǵ�ƽ����ϵ�ɵ�sin��PAB����õ�P��ֱ��AB�ľ���h=PAsin��PAB�����������䷽���ɶ��κ�������ֵ�������ɵõ��������ֵ��PA��PB��ֵ��
���  �⣺�������٣���$\frac{PA}{PB}$=$\frac{50}{30}$=$\frac{5}{3}$��
�⣺�������٣���$\frac{PA}{PB}$=$\frac{50}{30}$=$\frac{5}{3}$��
��PA=5x����PB=3x��
��cos��PAB=$\frac{25{x}^{2}+225-9{x}^{2}}{2��16��5x}$=$\frac{x}{10}$+$\frac{8}{5x}$��
��ͬ�ǵ�ƽ����ϵ�ɵ�sin��PAB=$\sqrt{1-��\frac{x}{10}+\frac{8}{5x}��^{2}}$��
���Ե�P��ֱ��AB�ľ���h=PAsin��PAB=5x•$\sqrt{1-��\frac{x}{10}+\frac{8}{5x}��^{2}}$
=$\sqrt{-\frac{1}{4}��{x}^{2}-34��^{2}+225}$��
��cos��PAB��1����$\frac{x}{10}$+$\frac{8}{5x}$��1����2��x��8��
���Ե�x2=34����x=$\sqrt{34}$ʱ��hȡ�����ֵ15ǧ�ף�
��ѡַӦ����PA=5$\sqrt{34}$ǧ�ף�PB=3$\sqrt{34}$ǧ�ף�
���� ���⿼��������ε���ѧģ�͵Ľⷨ��ע���������Ҷ�����ͬ�ǵ�ƽ����ϵ�Ͷ��κ�������ֵ�������黯�����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
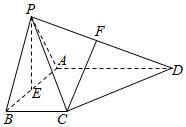 ��ͼ��������P-ABCD�У�AD��BC��AB��AD��E��AB���е㣬AB=AD=PA=PB=2��BC=1��PC=$\sqrt{5}$��
��ͼ��������P-ABCD�У�AD��BC��AB��AD��E��AB���е㣬AB=AD=PA=PB=2��BC=1��PC=$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABCD�У�����ABCDΪ���Σ�PA��ƽ��ABCD��EΪPD���е㣮
��ͼ��������P-ABCD�У�����ABCDΪ���Σ�PA��ƽ��ABCD��EΪPD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
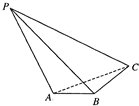 ������P-ABC�У�AB��BC��ƽ��PAB��ƽ��ABC��BC=2AB=1��PC=$\sqrt{3}$����PBA=$\frac{��}{4}$��
������P-ABC�У�AB��BC��ƽ��PAB��ƽ��ABC��BC=2AB=1��PC=$\sqrt{3}$����PBA=$\frac{��}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
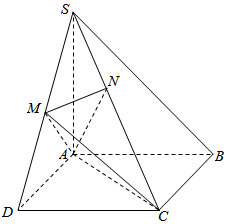 ��ͼ��������S-ABCD�У�����ABCD�������Σ�SA�͵���ABCD��SA=SB����M��SD���е㣬AN��SC���ҽ�SC�ڵ�N��
��ͼ��������S-ABCD�У�����ABCD�������Σ�SA�͵���ABCD��SA=SB����M��SD���е㣬AN��SC���ҽ�SC�ڵ�N���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
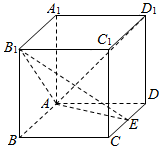 ��ͼ��ʾ���ڳ�����ABCD-A1B1C1D1�У�AA1=AD=1��EΪCD���е㣮
��ͼ��ʾ���ڳ�����ABCD-A1B1C1D1�У�AA1=AD=1��EΪCD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com