
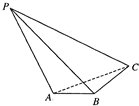
 在三棱锥P-ABC中,AB⊥BC,平面PAB⊥平面ABC,BC=2AB=1,PC=$\sqrt{3}$,∠PBA=$\frac{π}{4}$.
在三棱锥P-ABC中,AB⊥BC,平面PAB⊥平面ABC,BC=2AB=1,PC=$\sqrt{3}$,∠PBA=$\frac{π}{4}$.分析 (1)由已知推导出BC⊥平面PAB,由此能证明BC⊥PB.
(2)法一:以B为原点,BC为x轴,BA为y轴,过B作垂直于平面ABC的直线为z轴,建立空间直角坐标系,利用向量法能求出二面角A-PC-B的大小.
法二:作PQ⊥直线AB于Q,则PO⊥平面ABC,作AE⊥PB于E,则AE⊥平面PBC,∠AFE就是二面角A-PC-B的平面角,由此能求出二面角A-PC-B的大小.
解答 证明:(1)∵平面PAB⊥平面ABC,且AB⊥BC,
∴BC⊥平面PAB,
∴BC⊥PB.(4分)
(2)解法一:如图,以B为原点,BC为x轴,BA为y轴,过B作垂直于平面ABC的直线为z轴,建立空间直角坐标系,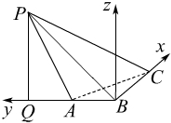
则$A(0,\frac{1}{2},0),B(0,0,0),C(1,0,0)$,(6分)
∵平面PAB⊥平面ABC,∴点P在坐标平面yBz内,
∵PC=$\sqrt{3}$,BC=1,BC⊥PB,∴$PB=\sqrt{2}$,
作PQ垂直于直线AB于Q,
则$PQ=PB•sin∠PBA=\sqrt{2}•sin\frac{π}{4}=1$,QB=1,
∴P(0,1,1),$\overrightarrow{BP}=(0,1,1)$,$\overrightarrow{PC}=(1,-1,-1)$,$\overrightarrow{AC}=(1,-\frac{1}{2},0)$,(8分)
设平面PBC的法向量为$\overrightarrow{n_1}=(x,y,z)$,
则$\left\{\begin{array}{l}{n_1}•\overrightarrow{BP}=0\\{n_1}•\overrightarrow{PC}=0\end{array}\right.⇒\left\{\begin{array}{l}y+z=0\\ x-y-z=0\end{array}\right.$,取y=1,得$\overrightarrow{n_1}=(0,1,-1)$,
设平面PAC的法向量$\overrightarrow{{n}_{2}}$=(a.b.c),
$\overrightarrow{PA}$=(0,-$\frac{1}{2}$,-1),$\overrightarrow{PC}$=(1,-1,-1),
则$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}•\overrightarrow{PA}=-\frac{1}{2}b-c=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{PC}=a-b-c=0}\end{array}\right.$,取a=1,得$\overrightarrow{n_2}=(1,2,-1)$,(10分)
∴$cos<\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}>$=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}|•|\overrightarrow{{n}_{2}}|}$=$\frac{\sqrt{3}}{2}$,
由图知,二面角A-PC-B是锐二面角,
∴二面角A-PC-B的大小是$\frac{π}{6}$.(12分)
解:(2)解法二: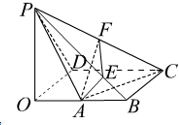 作PQ⊥直线AB于Q,则PQ⊥平面ABC,
作PQ⊥直线AB于Q,则PQ⊥平面ABC,
∵$∠PBA=\frac{π}{4}$,$PB=\sqrt{2}$,PO=BO=1,
如图,作AE⊥PB于E,则AE⊥平面PBC,
∴AE⊥PC,取PC中点F,连接AF,EF,
∵AO=AB=$\frac{1}{2}$,PO=BC=1,
∴$AP=AC=\frac{{\sqrt{5}}}{2}$,∴AF⊥PC,∴PC⊥平面AEF,
∴PC⊥EF,∴∠AFE就是二面角A-PC-B的平面角.(8分)
$AF=\sqrt{A{P^2}-P{F^2}}=\frac{{\sqrt{2}}}{2}$,$AE=\frac{{\sqrt{2}}}{2}AB=\frac{{\sqrt{2}}}{4}$,
∴$sin∠AFE=\frac{AE}{AF}=\frac{1}{2}$,$∠AFE=\frac{π}{6}$,
∴二面角A-PC-B的大小是$\frac{π}{6}$.(12分)
点评 本题考查异面直线垂直的证明,考查二面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
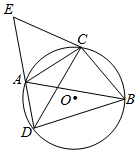 如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.
如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD⊥AB,AB∥DC,PA⊥底面ABCD,点E为棱PC的中点.AD=DC=AP=2AB=2.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD⊥AB,AB∥DC,PA⊥底面ABCD,点E为棱PC的中点.AD=DC=AP=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,A,B是两个垃圾中转站,B在A的正东方向16千米处,AB的南面为居民生活区.为了妥善处理生活垃圾,政府决定在AB的北面建一个垃圾发电厂P.垃圾发电厂P的选址拟满足以下两个要求(A,B,P可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点P到直线AB的距离要尽可能大).现估测得A,B两个中转站每天集中的生活垃圾量分别约为30吨和50吨,问垃圾发电厂该如何选址才能同时满足上述要求?
如图所示,A,B是两个垃圾中转站,B在A的正东方向16千米处,AB的南面为居民生活区.为了妥善处理生活垃圾,政府决定在AB的北面建一个垃圾发电厂P.垃圾发电厂P的选址拟满足以下两个要求(A,B,P可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点P到直线AB的距离要尽可能大).现估测得A,B两个中转站每天集中的生活垃圾量分别约为30吨和50吨,问垃圾发电厂该如何选址才能同时满足上述要求?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
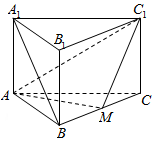 如图,已知三棱柱A1B1C1-ABC中,侧棱与底面垂直,AB=BC=AA1,∠ABC=90°,M是BC的中点.
如图,已知三棱柱A1B1C1-ABC中,侧棱与底面垂直,AB=BC=AA1,∠ABC=90°,M是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一艘船在航行过程中发现前方的河道上有一座圆拱桥.在正常水位时,拱桥最高点距水面8m,拱桥内水面宽32m,船只在水面以上部分高6.5m,船顶部宽8m,故通行无阻,如图所示.
一艘船在航行过程中发现前方的河道上有一座圆拱桥.在正常水位时,拱桥最高点距水面8m,拱桥内水面宽32m,船只在水面以上部分高6.5m,船顶部宽8m,故通行无阻,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
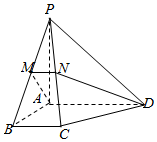 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
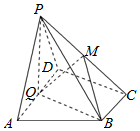 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com