
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)问题转化为k>$\frac{lnx}{x}$ 在R+上恒成立,设g(x)=$\frac{lnx}{x}$(x>0),根据函数的单调性求出g(x)的最大值,从而求出k的范围即可;
(3)根号g(x)的单调性,得到即$\frac{{\frac{1}{x_1}ln({\frac{1}{x_1}+\frac{1}{x_2}})}}{{\frac{1}{x_1}+\frac{1}{x_2}}}>ln\frac{1}{x_1}$,$\frac{{\frac{1}{x_2}ln({\frac{1}{x_1}+\frac{1}{x_2}})}}{{\frac{1}{x_1}+\frac{1}{x_2}}}>ln\frac{1}{x_2}$,相加整理即可.
解答 解:(1)函数f(x)的定义域为(0,+∞),
${f^/}(x)=\frac{1}{x}-1$….(1分)
∵${f^/}(x)=\frac{1}{x}-1>0$,∴0<x<1,
∵${f^/}(x)=\frac{1}{x}-1<0$,∴x>1….(2分)
故函数f(x)的递增区间为(0,1),递减区间为(1,+∞)….(3分)
(2)欲使f(x)<2?lnx-kx<0<在R+上恒成立,
只需k>$\frac{lnx}{x}$ 在R+上恒成立….(4分)
设g(x)=$\frac{lnx}{x}$(x>0),g′(x)=$\frac{1-lnx}{{x}^{2}}$,
x∈(0,e),g′(x)>0,g(x)为增函数,
x∈(e,+∞),g′(x)<0,g(x)为减函数,
∴x=e时,g(e)=$\frac{1}{e}$是最大值,
只需$\frac{1}{e}$<k,即k>$\frac{1}{e}$…(6分)
(3)∵$e>\frac{1}{x_1}+\frac{1}{x_2}>\frac{1}{x_1}>0$由(2)可知g(x)在(0,e)上单调增,…(7分)
$\frac{{ln({\frac{1}{x_1}+\frac{1}{x_2}})}}{{\frac{1}{x_1}+\frac{1}{x_2}}}>\frac{{ln\frac{1}{x_1}}}{{\frac{1}{x_1}}}$,即$\frac{{\frac{1}{x_1}ln({\frac{1}{x_1}+\frac{1}{x_2}})}}{{\frac{1}{x_1}+\frac{1}{x_2}}}>ln\frac{1}{x_1}$,
同理$\frac{{\frac{1}{x_2}ln({\frac{1}{x_1}+\frac{1}{x_2}})}}{{\frac{1}{x_1}+\frac{1}{x_2}}}>ln\frac{1}{x_2}$…(9分)
相加得 $\frac{{({\frac{1}{x_1}+\frac{1}{x_2}})ln({\frac{1}{x_1}+\frac{1}{x_2}})}}{{\frac{1}{x_1}+\frac{1}{x_2}}}>ln\frac{1}{x_1}+ln\frac{1}{x_2}$,
∴$ln({\frac{1}{x_1}+\frac{1}{x_2}})>ln\frac{1}{{{x_1}{x_2}}}$,
得:x1+x2>1.…(10分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查不等式的证明,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (1,+∞) | C. | (0,1) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
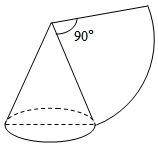
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
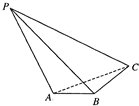 在三棱锥P-ABC中,AB⊥BC,平面PAB⊥平面ABC,BC=2AB=1,PC=$\sqrt{3}$,∠PBA=$\frac{π}{4}$.
在三棱锥P-ABC中,AB⊥BC,平面PAB⊥平面ABC,BC=2AB=1,PC=$\sqrt{3}$,∠PBA=$\frac{π}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com