
分析 (1)设事件A表示“投掷一次骰子甲得一分”,事件B表示“投掷一次骰子乙得一分”,事件C表示“投掷一次骰子丙得一分”,由已知得P(A)=$\frac{1}{6}$,P(B)=$\frac{1}{3}$,P(C)=$\frac{1}{2}$,从而能求出x=0,y=1,z=2的概率.
(2)X=0,1,2,3; Y=0,1,2,3; Z=0,1,2,3.但是只得3次分,因而必须满足X+Y+Z=3,随机变量ξ的样本空间为{0,1,2,3},事实上ξ=3-Y,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答 解:(1)设事件A表示“投掷一次骰子甲得一分”,事件B表示“投掷一次骰子乙得一分”,事件C表示“投掷一次骰子丙得一分”,
则P(A)=$\frac{1}{6}$,P(B)=$\frac{1}{3}$,P(C)=$\frac{1}{2}$,
∴x=0,y=1,z=2的概率p=($\frac{5}{6}$)3C${\;}_{3}^{1}$($\frac{1}{3}$)($\frac{2}{3}$)2${C}_{3}^{2}(\frac{1}{2})^{2}(\frac{1}{2})$=$\frac{125}{1296}$.
(2)X=0,1,2,3; Y=0,1,2,3; Z=0,1,2,3.
但是只得3次分,因而必须满足X+Y+Z=3,随机变量ξ的样本空间为{0,1,2,3}
事实上ξ=3-Y,
∴P(ξ=0)=P(Y=3)=($\frac{1}{3}$)3=$\frac{1}{27}$,
P(ξ=1)=P(Y=2)=${C}_{3}^{2}(\frac{1}{3})^{2}(\frac{2}{3})$=$\frac{2}{9}$,
P(ξ=2)=P(Y=1)=${C}_{3}^{1}(\frac{1}{3})(\frac{2}{3})^{2}$=$\frac{4}{9}$,
P(ξ=3)=P(Y=0)=($\frac{2}{3}$)3=$\frac{8}{27}$,
∴ξ的分布列:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{27}$ | $\frac{2}{9}$ | $\frac{4}{9}$ | $\frac{8}{27}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意n次重复试验中事件A恰好发生k次的概率计算公式的合理运用.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
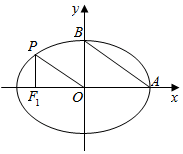 如图,椭圆$\frac{x^2}{a^2$+$\frac{y^2}{b^2}$=1(a>b>0)与x轴、y轴的正半轴相交于A、B,过椭圆上一点P作x轴的垂线,垂足恰为左焦点F1,OP∥AB.
如图,椭圆$\frac{x^2}{a^2$+$\frac{y^2}{b^2}$=1(a>b>0)与x轴、y轴的正半轴相交于A、B,过椭圆上一点P作x轴的垂线,垂足恰为左焦点F1,OP∥AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 身高一定是146cm | B. | 身高在146cm以上 | C. | 身高在146cm以下 | D. | 身高在146cm左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD⊥AB,AB∥DC,PA⊥底面ABCD,点E为棱PC的中点.AD=DC=AP=2AB=2.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD⊥AB,AB∥DC,PA⊥底面ABCD,点E为棱PC的中点.AD=DC=AP=2AB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com