
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 随机变量X服从正态分布N(2,σ2),所以μ=2,即函数f(x)的图象关于直线x=2对称,因为${∫}_{0}^{2}$f(x)dx=$\frac{1}{3}$,所以P(0<X≤2)=$\frac{1}{3}$,利用图象的对称性,即可得出结论.
解答 解:因为随机变量X服从正态分布N(2,σ2),所以μ=2,即函数f(x)的图象关于直线x=2对称,
因为${∫}_{0}^{2}$f(x)dx=$\frac{1}{3}$,所以P(0<X≤2)=$\frac{1}{3}$,
所以P(2<X≤4)=$\frac{1}{3}$,
所以P(X>4)=$\frac{1}{2}-\frac{1}{3}$=$\frac{1}{6}$,
故选:A.
点评 本题考查正态分布,考查图象的对称性,考查学生的计算能力,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 身高一定是146cm | B. | 身高在146cm以上 | C. | 身高在146cm以下 | D. | 身高在146cm左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱锥ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1⊥底面ABC,AA1=$\frac{\sqrt{3}}{2}$,P、Q分别是AB、AC上的点,且PQ∥BC.
在三棱锥ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1⊥底面ABC,AA1=$\frac{\sqrt{3}}{2}$,P、Q分别是AB、AC上的点,且PQ∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
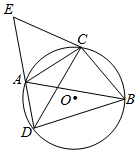 如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.
如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一艘船在航行过程中发现前方的河道上有一座圆拱桥.在正常水位时,拱桥最高点距水面8m,拱桥内水面宽32m,船只在水面以上部分高6.5m,船顶部宽8m,故通行无阻,如图所示.
一艘船在航行过程中发现前方的河道上有一座圆拱桥.在正常水位时,拱桥最高点距水面8m,拱桥内水面宽32m,船只在水面以上部分高6.5m,船顶部宽8m,故通行无阻,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com