
【题目】平面直角坐标系 ![]() 中,倾斜角为
中,倾斜角为 ![]() 的直线
的直线 ![]() 过点
过点 ![]() ,以原点
,以原点 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)写出直线 ![]() 的参数方程(
的参数方程( ![]() 为常数)和曲线
为常数)和曲线 ![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线 ![]() 与
与 ![]() 交于
交于 ![]() 、
、 ![]() 两点,且
两点,且 ![]() ,求倾斜角
,求倾斜角 ![]() 的值.
的值.
【答案】
(1)解:直线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),
为参数),
曲线 ![]() 的直角坐标方程:
的直角坐标方程: ![]()
(2)解:把直线的参数方程代入 ![]() ,得
,得 ![]() ,
,![]() ,
, ![]() ,
,
根据直线参数的几何意义, ![]() ,
,
得 ![]() 或
或 ![]() .
.
又因为 ![]() ,
,
所以 ![]() .
.
【解析】(1)结合直角坐标系中直线的特征求得直线l的参数方程,求曲线C的直角坐标方程时先利用极坐标系将曲线C的方程化为参数方程,再求得其直角坐标方程;(2)利用交点的特征表示出点A,B坐标之间的关系,再根据直线参数的几何意义表示出两个模长的积,从而求得α的值,同时需根据点A,B的存在性判断α是否适合.
【考点精析】本题主要考查了极坐标系和直线的参数方程的相关知识点,需要掌握平面内取一个定点O,叫做极点;自极点O引一条射线OX叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系;经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为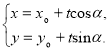 (
(![]() 为参数)才能正确解答此题.
为参数)才能正确解答此题.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,
时,![]() 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(2)是否存在整数a、b(其中a、b是常数,且a<b),使得关于x的不等式![]() 的解集为
的解集为![]() ?若存在,求出a、b的值,若不存在,请说明理由.
?若存在,求出a、b的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( ) 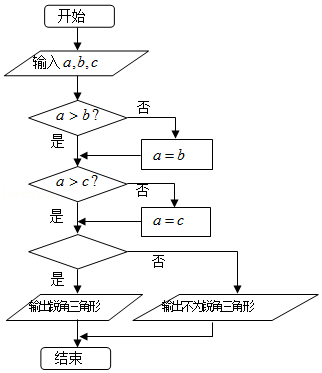
A.a2+b2>c2?
B.a2+c2>b2?
C.b2+c2>a2?
D.b2+a2=c2?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋内装有6个球,这些球依次被编号为1、2、3、……、6,设编号为n的球重n2-6n+12(单位:克),这些球等可能地从袋里取出(不受重量、编号的影响).
(1)从袋中任意取出一个球,求其重量大于其编号的概率;
(2)如果不放回地任意取出2个球,求它们重量相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PC⊥底面ABCD,AD∥BC,AD=2BC=2,PC=2,△ABC是以AC为斜边的等腰直角三角形,E是PD的中点.
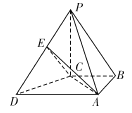
(1)求证:平面EAC⊥平面PCD;
(2)求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点(1,13),且函数
的图象过点(1,13),且函数![]()
![]() 是偶函数.
是偶函数.
(1)求![]() 的解析式;
的解析式;
(2)已知![]() ,
,![]() ,求函数
,求函数![]() 在[
在[![]() ,2]上的最大值和最小值;
,2]上的最大值和最小值;
(3)函数![]() 的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在(﹣∞,0)上的可导函数,其导函数为f′(x),且有xf′(x)>x2+3f(x),则不等式8f(x+2014)+(x+2014)3f(﹣2)>0的解集为( )
A.(﹣∞,﹣2016)
B.(﹣2018,﹣2016)
C.(﹣2018,0)
D.(﹣∞,﹣2018)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com