Question

19．如图，顶点在坐标原点的抛物线经过点A（-4，4），△BCD的三个顶点B（0，0），C（0，2），D（2，0）．
（1）求该抛物线的表达式和直线AC的表达式；
（2）若将△BCD沿射线CA方向平移$\sqrt{5}$个单位长度后得到△B′C′D′
①请判断此时直角顶点B′是否落在此抛物线上；
②求平移过程中三角形所扫过的面积；
③将△B′C′D′绕平面内其一点逆时针旋转90°，使得旋转后的三角形的两个顶点落在抛物线上，请直接写出旋转中心的坐标．

Answer 1

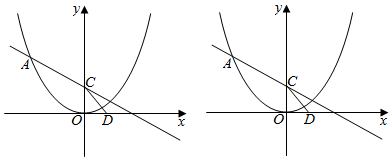
分析 （1）设抛物线的方程为y=ax²，代入（-4，4），解方程可得；
（2）①由题意可得B'在直线y=-$\frac{1}{2}$x上，求得B'的坐标，代入即可判断；
②平移过程中三角形所扫过的面积为平行四边形BCC'B'和三角形BCD的面积之和．计算即可得到所求值；
③设旋转后的三角形为△B''C''D''，有三种情况：当B''，C''在抛物线上；当B''，D''在抛物线上；当C''，D''在抛物线上，即可得到所求中心的坐标．

解答 解：（1）设抛物线的方程为y=ax²，
代入（-4，4），可得4=16a，解得a=$\frac{1}{4}$，
即抛物线的方程为y=$\frac{1}{4}$x²；
直线AC的方程为y=-$\frac{1}{2}$x+2；
（2）①由题意可得B'在直线y=-$\frac{1}{2}$x上，
且|B'B|=$\sqrt{5}$，可得B'（-2，1），
即有B'在抛物线上；
②平移过程中三角形所扫过的面积为：平行四边形BCC'B'和三角形BCD的面积之和．
由两平行线y=-$\frac{1}{2}$x和y=-$\frac{1}{2}$x+2的距离为$\frac{|2|}{\sqrt{1+\frac{1}{4}}}$=$\frac{4}{\sqrt{5}}$，
可得所求面积为$\sqrt{5}$•$\frac{4}{\sqrt{5}}$+$\frac{1}{2}$•2•2=6；
③设旋转后的三角形为△B''C''D''，
有三种情况：当B''，C''在抛物线上，可得B''C''平行于x轴，
可得旋转中心为（0，2）；
当B''，D''在抛物线上，则B''D''平行于y轴，由抛物线的性质，可得不存在；
当C''，D''在抛物线上，则C''D''的斜率为-1，
可得旋转中心为（$\frac{1}{8}$，$\frac{25}{8}$）．
综上可得，旋转中心为（0，2），（$\frac{1}{8}$，$\frac{25}{8}$）．

点评 本题考查抛物线的方程的求法，注意运用待定系数法，考查扫过图形的面积的求法，注意观察由平行四边形和三角形的面积可得，同时考查旋转中心的求法，注意运用讨论的思想方法，借助数形结合，属于中档题．