练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知等差数列{an}的前n项和为Sn，S13＞0，S14＜0，若atat+1＜0，则t=7．

    分析 解：根据等差数列{an}的前n项和公式，利用项的性质，列出不等式组，求出a7＞0，a8＜0，即得t的值．

    解答 解：根据题意，S13＞0，S14＜0，
    得$\left\{\begin{array}{l}{{S}_{13}=\frac{13{（a}_{1}{+a}_{13}）}{2}＞0}\\{{S}_{14}=\frac{14{（a}_{1}{+a}_{14}）}{2}＜0}\end{array}\right.$，
    即$\left\{\begin{array}{l}{{a}_{1}{+a}_{13}＞0}\\{{a}_{1}{+a}_{14}＜0}\end{array}\right.$，
    ∴$\left\{\begin{array}{l}{{a}_{1}{+a}_{13}={2a}_{7}＞0}\\{{a}_{1}{+a}_{14}{=a}_{7}{+a}_{8}＜0}\end{array}\right.$，
    ∴$\left\{\begin{array}{l}{{a}_{7}＞0}\\{{a}_{8}＜0}\end{array}\right.$；
    又atat+1＜0，
    ∴t=7．

    点评 本题考查了等差数列{an}的前n项和公式与项的性质的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．如果两条直线l1：ax+2y+6=0与l2：x+（a-1）y+3=0平行，那么实数a等于（　　）
    A．-1B．2C．2或-1D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．设$\overrightarrow{a}$=（-2，3），$\overrightarrow{b}$=（-8，5），则5$\overrightarrow{a}$-3$\overrightarrow{b}$=（14，0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．函数y=$\frac{x-cosx}{x+sinx}$在x=2处的导数是$\frac{3sin2+1-cos2}{（2+sin2）^{2}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，则下列关系正确的是（　　）
    A．|$\overrightarrow{a}•\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|B．|$\overrightarrow{a}•\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$|
    C．|$\overrightarrow{a}•\overrightarrow{b}$|≥|$\overrightarrow{a}$||$\overrightarrow{b}$|D．以上答案都不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．如图，顶点在坐标原点的抛物线经过点A（-4，4），△BCD的三个顶点B（0，0），C（0，2），D（2，0）．
    （1）求该抛物线的表达式和直线AC的表达式；
    （2）若将△BCD沿射线CA方向平移$\sqrt{5}$个单位长度后得到△B′C′D′
    ①请判断此时直角顶点B′是否落在此抛物线上；
    ②求平移过程中三角形所扫过的面积；
    ③将△B′C′D′绕平面内其一点逆时针旋转90°，使得旋转后的三角形的两个顶点落在抛物线上，请直接写出旋转中心的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．命题p：?a∈（-∞，-$\frac{1}{4}$]，使得函数f（x）=|2x+$\frac{a}{{2}^{x}}$|在[-$\frac{1}{2}$，3]上单调递增；命题q：?a∈[2，+∞），直线2x+y=0与双曲线$\frac{{y}^{2}}{{a}^{2}}$-x2=1（a＞0）相交．则下列命题中正确的是（　　）
    A．￢pB．p∧qC．（￢p）∨qD．p∧（￢q）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在数列{an}中，an+1=an+t（n∈N*），其前n项和Sn=A•n2+B•n+c，则实数c为（　　）
    A．-1B．0C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

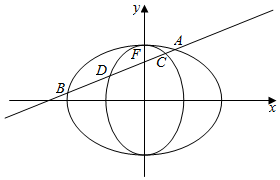    6．如图的椭圆C1，C2的离心率相等，中心均为坐标原点，焦点分别在x轴和y轴上，且两椭圆都过点（0，$\sqrt{2}$），设点F是椭圆C2的上焦点，过点F的动直线l交椭圆C1于A，B两点，交椭圆C2于C，D两点，当直线l经过椭圆C1的左焦点时，$\frac{|AB|}{|CD|}$=$\frac{5\sqrt{2}}{4}$．
    （1）求椭圆C1，C2的标准方程；
    （2）平面内是否存在与点F不同的定点P，使得∠APC=∠BPD恒成立？若存在，求出定点P的坐标，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案