
分析 求导y′=$\frac{(x-cosx)′(x+sinx)-(x-cosx)(x+sinx)^{′}}{(x+sinx)^{2}}$=$\frac{(1+sinx)(x+sinx)-(x-cosx)(1+cosx)}{(x+sinx)^{2}}$,代入x=2化简即可.
解答 解:y′=$\frac{(x-cosx)′(x+sinx)-(x-cosx)(x+sinx)^{′}}{(x+sinx)^{2}}$
=$\frac{(1+sinx)(x+sinx)-(x-cosx)(1+cosx)}{(x+sinx)^{2}}$
=$\frac{sinx+xsinx+1-xcosx+cosx}{(x+sinx)^{2}}$,
故y′|x=2=$\frac{3sin2+1-cos2}{(2+sin2)^{2}}$,
故答案为:$\frac{3sin2+1-cos2}{(2+sin2)^{2}}$.
点评 本题考查了导数的运算及学生的化简运算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
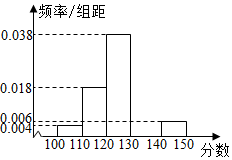 2015-2016学年高二A班50名学生在其中数学测试中(满分150分),成绩都介于100分到150分之间,将测试结果按如下方式分成五组,第一组[100,110),第二组[110,120),…,第五组[140,150),按上述分组方法得到的频率分布直方图如图所示,
2015-2016学年高二A班50名学生在其中数学测试中(满分150分),成绩都介于100分到150分之间,将测试结果按如下方式分成五组,第一组[100,110),第二组[110,120),…,第五组[140,150),按上述分组方法得到的频率分布直方图如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-2=0 | B. | x+y+2$\sqrt{2}$=0 | C. | x-y-2=0 | D. | x-y-2$\sqrt{2}$=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com