
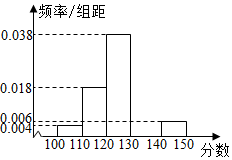
 2015-2016ѧ��߶�A��50��ѧ����������ѧ�����У�����150�֣����ɼ�������100�ֵ�150��֮�䣬�����Խ�������·�ʽ�ֳ����飬��һ��[100��110�����ڶ���[110��120��������������[140��150�������������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
2015-2016ѧ��߶�A��50��ѧ����������ѧ�����У�����150�֣����ɼ�������100�ֵ�150��֮�䣬�����Խ�������·�ʽ�ֳ����飬��һ��[100��110�����ڶ���[110��120��������������[140��150�������������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������ ��1����Ƶ�ʷֲ�ֱ��ͼ����������Ƶ�ʣ���Ƶ�ʷֲ�ֱ��ͼ�����������ɣ�
��2������Ƶ�ʷֲ�ֱ��ͼ������ɼ���[110��130���ڵ��������ɣ�
��3����Ƶ�ʷֲ�ֱ��ͼ�ó��������ڵ����飬�Ӷ����������ֵ��
�ٸ�����λ������Ƶ����������λ����
��� 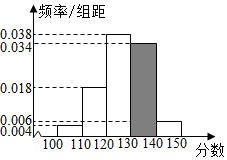 �⣺��1����Ƶ�ʷֲ�ֱ��ͼ�ã��������Ƶ��Ϊ1-��0.004+0.018+0.038+0.006����10=1-0.66=0.34��
�⣺��1����Ƶ�ʷֲ�ֱ��ͼ�ã��������Ƶ��Ϊ1-��0.004+0.018+0.038+0.006����10=1-0.66=0.34��
��Ƶ�ʷֲ�ֱ��ͼ�������������£�
��2������Ƶ�ʷֲ�ֱ��ͼ�ã��ɼ���[110��130���ڵ�����Ϊ��
50��0.018��10+50��0.038��10=28
���Ըð��������ѧ�����гɼ�Ϊ���õ�����Ϊ28��
��3����Ƶ�ʷֲ�ֱ��ͼ֪�������ڵ�����[120��130���ڣ�
����������$\frac{120+130}{2}$=125��
��Ϊ�������ڵ�һ���ڶ����Ƶ��Ϊ10����0.004+0.018��=0.22��0.5��
�������ڵ�һ���ڶ����������Ƶ��Ϊ10����0.004+0.018+0.038��=0.6��0.5��
������λ�����ڵ������У�����λ��Ϊx��0.22+��x-120����0.038=0.5��
���x��127.4��
���ԣ������������ݵ�������125����λ����127.4��
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�����⣬Ҳ��������������λ���ļ������⣬�ǻ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 2 | C�� | 2��-1 | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��a+b����f��a�� | B�� | f��a+b����f��a��+f��b�� | C�� | f��a+b����a+b | D�� | f��a+b����f��a��+f��b�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
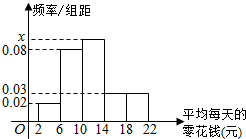 Ϊ���˽�ѧ��ƽ��ÿ���㻨Ǯ��������Ǯ��ȡ����Ԫ�����Ա�����ѧ��������ȷ�����ѹۣ�ijУ�Ӹ�һ�꼶1000��ѧ���������ȡ100�������˵��飬������������������Ƶ�ʷֲ�ֱ��ͼ����ͼ�����ݴ˹��Ƹ�һ�꼶ÿ���㻨Ǯ��[6��14���ڵ�ѧ����Ϊ��������
Ϊ���˽�ѧ��ƽ��ÿ���㻨Ǯ��������Ǯ��ȡ����Ԫ�����Ա�����ѧ��������ȷ�����ѹۣ�ijУ�Ӹ�һ�꼶1000��ѧ���������ȡ100�������˵��飬������������������Ƶ�ʷֲ�ֱ��ͼ����ͼ�����ݴ˹��Ƹ�һ�꼶ÿ���㻨Ǯ��[6��14���ڵ�ѧ����Ϊ��������| A�� | 780 | B�� | 680 | C�� | 648 | D�� | 460 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com